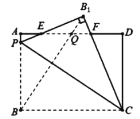
题目内容
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 上一动点(
上一动点(![]() 与
与![]() 不重合),将
不重合),将![]() 沿
沿![]() 翻折至
翻折至![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,若
,若![]() ,则
,则![]() 的长=______,折痕
的长=______,折痕![]() 的长_____.
的长_____.
【答案】5 ![]()
【解析】
根据折叠及矩形的性质得到∠B1QF =∠CB1B,即可得到QF= B1F=5,如图,过点Q作QH⊥PB1于点H,得到△EHQ∽△EB1F,利用相似比得到EH,QH,从而得到B1H及B1Q,计算出cos∠HB1Q= ,根据等量代换得到∠PB1B=∠PBB1=∠PCB,利用cos∠PCB = cos∠HB1Q=
,根据等量代换得到∠PB1B=∠PBB1=∠PCB,利用cos∠PCB = cos∠HB1Q=![]() 即可计算得出PC的值.
即可计算得出PC的值.
解:由折叠可知,PC 垂直平分BB1,
∴BC=B1C,BP=B1P,
∴∠CBB1=∠CB1B,∠PBB1=∠PB1B
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CBB1=∠B1QF,
∴∠B1QF =∠CB1B,
∴QF= B1F,
∵![]() ,
,
∴B1F=5,EF=13,
∴![]() ,
,
如图,过点Q作QH⊥PB1于点H,
∵∠PB1C=90°,
∴QH∥B1F,
∴△EHQ∽△EB1F,
∴![]() ,
,
即![]() ,
,
∴EH=![]() ,QH=
,QH=![]() ,
,
∴B1H=![]()
∴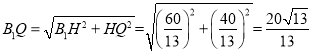 ,
,
∴cos∠HB1Q=
又∵∠PBB1+∠BPC=90°,∠BPC+∠PCB=90°,
∴∠PB1B=∠PBB1=∠PCB,
∴cos∠PCB = cos∠HB1Q=![]()
又∵![]() ,
,
∴cos∠PCB![]() ,即
,即![]() ,
,
∴PC=![]() ,
,
故答案为:5,![]()


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目