Question

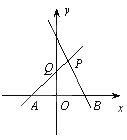
【题目】如图，在平面直角坐标系中，已知点A（1，3）、B（3，3）、C（4，2）．

（1）请在图中作出经过点A、B、C三点的⊙M，并写出圆心M的坐标；
（2）若D（1，4），则直线BD与⊙M ．
A.相切
B.相交．

Answer 1

【答案】
（1）解：如图所示：

圆心M的坐标为（2，1）；

（2）A
【解析】（2）连接MB，DB，DM，
∵DB= ，BM= ，DM= ，
∴DB2+BM2=DM2 ，
∴△DBM是直角三角形，
∴∠DBM=90°，
即BM⊥DB，
∴直线BD与⊙M相切，
故选A．
【考点精析】本题主要考查了直线与圆的三种位置关系的相关知识点，需要掌握直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点才能正确解答此题．