题目内容
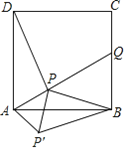
【题目】如图,点P是正方形ABCD内一点,连接AP并延长,交BC于点Q.连接DP.将△ADP绕点A顺时针旋转90°至△ABP'.连结PP',若AP=1,PB=2![]() ,PD=
,PD=![]() ,则正方形的边长为( )
,则正方形的边长为( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
【答案】D
【解析】
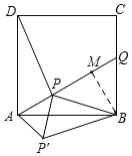
过点B作BM⊥AQ于点M,由折叠的性质可得DP=P'B=2![]() ,AP=AP'=1,∠PAP'=90°,由勾股定理和勾股定理的逆定理可求PP'=
,AP=AP'=1,∠PAP'=90°,由勾股定理和勾股定理的逆定理可求PP'=![]() ,∠APP'=45°,∠BPP'=90°,即可求∠BPM=180°-∠BPP'-∠APP'=45°,由勾股定理可求AB的长.
,∠APP'=45°,∠BPP'=90°,即可求∠BPM=180°-∠BPP'-∠APP'=45°,由勾股定理可求AB的长.
过点B作BM⊥AQ于点M,
∵将△ADP绕点A顺时针旋转90°至△ABP',
∴DP=P'B=2![]() ,AP=AP'=1,∠PAP'=90°,
,AP=AP'=1,∠PAP'=90°,
∴PP'=![]() ,∠APP'=45°,
,∠APP'=45°,
∵P'P2+PB2=2+8=10,P'B2=10,
∴P'P2+PB2=P'B2,
∴∠BPP'=90°,
∴∠BPM=180°-∠BPP'-∠APP'=45°,
∵BM⊥AQ,
∴∠BMP=90°,
∴∠PBM=90°-∠BPQ==45°,PM2+BM2=PB2,
∴∠PBM=∠BPM,
∴PM=BM,
又∵PB=2![]() ,PM2+BM2=PB2,
,PM2+BM2=PB2,
∴PM=BM=2,
∴AM=AP+PM=3,
∴AB=![]() ,
,
故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
次数 | 购买数量(件 | 购买总费用(元 | |
A | B | ||
第一次 | 2 | 1 | 55 |
第二次 | 1 | 3 | 65 |
根据以上信息解答下列问题:
(1)求A,B两种商品的单价;
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.