题目内容
【题目】(1)观察猜想
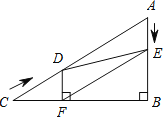
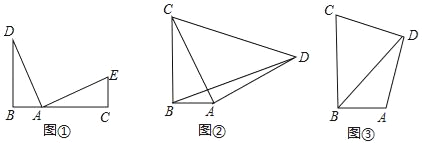
如图①点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°,AD=AE,则BC、BD、CE之间的数量关系为;
(2)问题解决
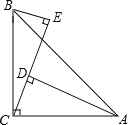
如图②,在Rt△ABC中,∠ABC=90°,CB=4,AB=2,以AC为直角边向外作等腰Rt△DAC,连结BD,求BD的长;
(3)拓展延伸
如图③,在四边形ABCD中,∠ABC=∠ADC=90°,CB=4,AB=2,DC=DA,请直接写出BD的长.
【答案】(1)BC=BD+CE,(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)证明△ADB≌△EAC,根据全等三角形的性质得到BD=AC,EC=AB,即可得到BC、BD、CE之间的数量关系;
(2)过D作DE⊥AB,交BA的延长线于E,证明△ABC≌△DEA,得到DE=AB=2,AE=BC=4,Rt△BDE中,BE=6,根据勾股定理即可得到BD的长;
(3)过D作DE⊥BC于E,作DF⊥AB于F,证明△CED≌△AFD,根据全等三角形的性质得到CE=AF,ED=DF,设AF=x,DF=y,根据CB=4,AB=2,列出方程组,求出
![]() 的值,根据勾股定理即可求出BD的长.
的值,根据勾股定理即可求出BD的长.
解:(1)观察猜想
结论: BC=BD+CE,理由是:
如图①,∵∠B=90°,∠DAE=90°,
∴∠D+∠DAB=∠DAB+∠EAC=90°,
∴∠D=∠EAC,
∵∠B=∠C=90°,AD=AE,
∴△ADB≌△EAC,
∴BD=AC,EC=AB,
∴BC=AB+AC=BD+CE;
(2)问题解决
如图②,过D作DE⊥AB,交BA的延长线于E,
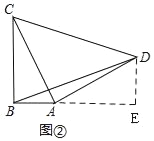
由(1)同理得:△ABC≌△DEA,
∴DE=AB=2,AE=BC=4,
Rt△BDE中,BE=6,
由勾股定理得: ![]()
(3)拓展延伸
如图③,过D作DE⊥BC于E,作DF⊥AB于F,
同理得:△CED≌△AFD,
∴CE=AF,ED=DF,
设AF=x,DF=y,
则![]() ,解得:
,解得:![]()
∴BF=2+1=3,DF=3,
由勾股定理得:![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案