��Ŀ����
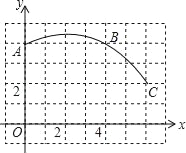
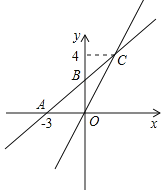
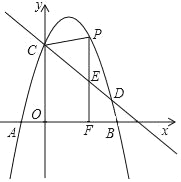
����Ŀ����ͼ��������y=��x2+bx+c��x�ύ�ڵ�A����1��0���͵�B����y�ύ��C��0��3����ֱ��y=![]() +m������C���������ߵ���һ����Ϊ��D����P��ֱ��CD�Ϸ��������ϵ�һ�����㣬����P��PF��x���ڵ�F����ֱ��CD�ڵ�E�����P�ĺ�����Ϊm��
+m������C���������ߵ���һ����Ϊ��D����P��ֱ��CD�Ϸ��������ϵ�һ�����㣬����P��PF��x���ڵ�F����ֱ��CD�ڵ�E�����P�ĺ�����Ϊm��
��1���������߽���ʽ�������D�����ꣻ
��2������PD����CDP������Ƿ�������ֵ�������ڣ��������������ֵ���������ڣ���˵�����ɣ�
��3������CPE�ǵ���������ʱ����ֱ��д��m��ֵ��
���𰸡���1��y=��x2+2x+3��D������Ϊ��![]() ������2����m=
������2����m=![]() ʱ����CDP������������ֵ�����ֵΪ
ʱ����CDP������������ֵ�����ֵΪ![]() ����3��m��ֵΪ
����3��m��ֵΪ![]() ��
��![]() ��
��![]() ��
��
��������
��1�����ô���ϵ�����������߽���ʽ��ֱ��CD�Ľ���ʽ��Ȼ��ⷽ���� ��D�����ꣻ
��D�����ꣻ
��2����P��m��-m2+2m+3������E��m��-![]() m+3������PE=-m2+
m+3������PE=-m2+![]() m�����������������ʽ�õ�S��PCD=
m�����������������ʽ�õ�S��PCD=![]() ��
��![]() ����-m2+
����-m2+![]() m��=-
m��=-![]() m2+
m2+![]() m��Ȼ�����ö��κ��������ʽ�����⣻
m��Ȼ�����ö��κ��������ʽ�����⣻
��3�����ۣ���PC=PEʱ��m2+��-m2+2m+3-3��2=��-m2+![]() m��2����CP=CEʱ��m2+��-m2+2m+3-3��2=m2+��-
m��2����CP=CEʱ��m2+��-m2+2m+3-3��2=m2+��-![]() m+3-3��2����EC=EPʱ��m2+��-
m+3-3��2����EC=EPʱ��m2+��-![]() m+3-3��2=��-m2+
m+3-3��2=��-m2+![]() m��2��Ȼ��ֱ�ⷽ�̼��ɵõ�����������m��ֵ��
m��2��Ȼ��ֱ�ⷽ�̼��ɵõ�����������m��ֵ��
��1����A����1��0����C��0��3���ֱ����y=��x2+bx+c��![]() �����
�����![]() ��
��
�������ߵĽ���ʽΪy=��x2+2x+3��
��C��0��3������y=��![]() x+n�����n=3��
x+n�����n=3��
��ֱ��CD�Ľ���ʽΪy=��![]() x+3��
x+3��
�ⷽ���� �����
�����![]()
��![]() ��
��
��D��������![]() ��
��![]() ����
����
��2�����ڣ�
��P��m����m2+2m+3������E��m����![]() m+3����
m+3����
��PE=��m2+2m+3������![]() m+3��=��m2+
m+3��=��m2+![]() m��
m��
��S��PCD=![]()
![]() ����m2+
����m2+![]() m��=��
m��=��![]() m2+
m2+![]() m=��
m=��![]() ��m��
��m��![]() ��2+
��2+![]() ��
��
��m=![]() ʱ����CDP������������ֵ�����ֵΪ
ʱ����CDP������������ֵ�����ֵΪ![]() ��
��
��3����PC=PEʱ��m2+����m2+2m+3��3��2=����m2+![]() m��2�����m=0����ȥ����m=
m��2�����m=0����ȥ����m=![]() ��
��
��CP=CEʱ��m2+����m2+2m+3��3��2=m2+����![]() m+3��3��2�����m=0����ȥ����m=
m+3��3��2�����m=0����ȥ����m=![]() ����ȥ����m=
����ȥ����m=![]() ��
��
��EC=EPʱ��m2+����![]() m+��3��2=����m2+
m+��3��2=����m2+![]() m��2�����m=
m��2�����m=![]() ����ȥ����m=
����ȥ����m=![]() ��
��
����������m��ֵΪ![]() ��
��![]() ��
��![]() ��
��

����Ŀ���߶����˶�Ա��һ��С����������һ���Ƕȵķ���������ڲ����ǿ��������������£�С��ķ��и߶�h��m�������ķ���ʱ�䣨s��������κ�����ϵ��t��h�ļ����Ӧֵ���±���ʾ��
t��s�� | 0 | 0.5 | 1 | 1.5 | 2 | �� |
h��m�� | 0 | 8.75 | 15 | 18.75 | 20 | �� |
��1����h��t֮��ĺ�����ϵʽ����Ҫ��дt��ȡֵ��Χ����
��2����С�����3sʱ�ĸ߶ȣ�