��Ŀ����
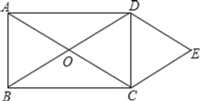
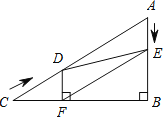
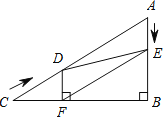
����Ŀ����ͼ����Rt��ABC�У���B��90����AC��60cm����A��60������D�ӵ�C������CA������4cm/s���ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2cm/s���ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����ts������D��DF��BC�ڵ�F������DE��EF��
��1����֤��AE��DF��
��2���ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ���˵�����ɣ�
��3����tΪ��ֵʱ����DEFΪֱ�������Σ���˵�����ɣ�
���𰸡���1������������2���ܣ�10����3����t��![]() ʱ��DEF��ֱ�������Σ���EDF��90��������t��12ʱ����DEF��ֱ�������Σ���DEF��90����
ʱ��DEF��ֱ�������Σ���EDF��90��������t��12ʱ����DEF��ֱ�������Σ���DEF��90����
��������
��1������t��ʾ��CD�Լ�AE�ij���Ȼ����ֱ�ǡ�CDF�У�����ֱ�������ε��������DF�ij�������֤����
��2����֤�ı���AEFD��ƽ���ı��Σ���AD��AEʱ���ı���AEFD�����Σ��ݴ˼����з������t��ֵ��
��3���ֱ�ӡ�EDF��90�����DEF��90������������ۼ������.
��1��֤��������Rt��ABC�У���B��90����AC��60cm����A��60����
���C��90������A��30����
��CD��4tcm��AE��2tcm��
�֡���ֱ�ǡ�CDF�У���C��30����
��DF��![]() CD��2tcm��
CD��2tcm��
��DF��AE��
��2���ܣ�
��DF��AB��DF��AE��
���ı���AEFD��ƽ���ı��Σ�
��AD��AEʱ���ı���AEFD�����Σ�
��60��4t��2t��
��ã�t��10��
����t��10ʱ��AEFD�����Σ�
��3���⣺��t��![]() ʱ��DEF��ֱ�������Σ���EDF��90������
ʱ��DEF��ֱ�������Σ���EDF��90������
��t��12ʱ����DEF��ֱ�������Σ���DEF��90������
�������£�
����EDF��90��ʱ��DE��BC��
���ADE����C��30����
��AD��2AE
��CD��4tcm��
��DF��AE��2tcm��
��AD��2AE��4tcm��
��4t+4t��60��
��t��![]() ʱ����EDF��90����
ʱ����EDF��90����
����DEF��90��ʱ��DE��EF��
���ı���AEFD��ƽ���ı��Σ�
��AD��EF��
��DE��AD��
���ADE��ֱ�������Σ���ADE��90����
�ߡ�A��60����
���DEA��30����
��AD��![]() AE��
AE��
AD��AC��CD��60��4t��cm����AE��DF��![]() CD��2tcm��
CD��2tcm��
��AD=tcm��
��60��4t��t��
���t��12��
������������t��![]() ʱ��DEF��ֱ�������Σ���EDF��90��������t��12ʱ����DEF��ֱ�������Σ���DEF��90����.
ʱ��DEF��ֱ�������Σ���EDF��90��������t��12ʱ����DEF��ֱ�������Σ���DEF��90����.

����Ŀ������ķ���������ij��˾�¹�Ʊ![]() �ɣ�ÿ��
�ɣ�ÿ��![]() Ԫ���±�Ϊ������ÿ�ոùɵ��ǵ���������������չ������У�����λ��Ԫ��
Ԫ���±�Ϊ������ÿ�ոùɵ��ǵ���������������չ������У�����λ��Ԫ��
���� | һ | �� | �� | �� | �� |
ÿ���ǵ� | +1.5 | ��0.7 | ��1.2 | +2 | ��1.8 |
��1������������ʱ��ÿ���Ƕ���Ԫ��
��2��������ÿ����۶���Ԫ����ͼ��Ƕ���Ԫ��
��3����֪��ķ�����Ʊʱ����![]() �������ѣ�����ʱ���踶�ɽ���
�������ѣ�����ʱ���踶�ɽ���![]() �������Ѻ͵�
�������Ѻ͵�![]() ����˰�������ķ������������ǰ��ȫ����Ʊ�������������������Σ�
����˰�������ķ������������ǰ��ȫ����Ʊ�������������������Σ�