题目内容
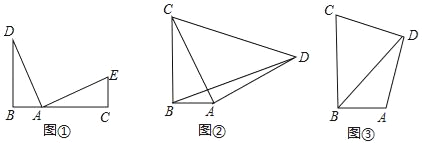
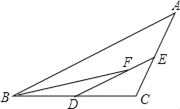
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为边
为边![]() 上的两个点,且
上的两个点,且![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)![]() 的度数会随着
的度数会随着![]() 度数的变化而变化吗?请说明理由.
度数的变化而变化吗?请说明理由.

【答案】(1)35°;(2)![]() 的度数不会随着
的度数不会随着![]() 度数的变化而变化,是35°.
度数的变化而变化,是35°.
【解析】
(1)根据等腰三角形性质求出∠ACE=∠AEC,∠BCD=∠BDC,得∠BCE=∠ACB-∠ACE =110°-75°=35°;再根据∠DCE=∠BCD-∠BCE可得;
(2)解题方法如(1),求∠ACE=∠AEC=![]() ;∠BCD=∠BDC=
;∠BCD=∠BDC=![]() ,∠BCE=∠ACB-∠ACE,所以∠DCE=∠BCD-∠BCE=
,∠BCE=∠ACB-∠ACE,所以∠DCE=∠BCD-∠BCE=![]() -(110°-
-(110°-![]() ).
).
因为![]() ,
,![]()
所以∠ACE=∠AEC=![]() ;
;
∠BCD=∠BDC=![]()
所以∠BCE=∠ACB-∠ACE=110°-75°=35°
所以∠DCE=∠BCD-∠BCE=70°-35°=35°;
(2)![]() 的度数不会随着
的度数不会随着![]() 度数的变化而变化,理由:
度数的变化而变化,理由:
因为在![]() 中,
中,![]() ,
,
所以![]()
因为![]() ,
,![]()
所以∠ACE=∠AEC=![]() ;
;
∠BCD=∠BDC=![]()
所以∠BCE=∠ACB-∠ACE=110°-![]()
所以∠DCE=∠BCD-∠BCE=![]() -(110°-
-(110°-![]() )=35°
)=35°
故![]() 的度数不会随着
的度数不会随着![]() 度数的变化而变化,是35°.
度数的变化而变化,是35°.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
【题目】高尔夫运动员将一个小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间(s)满足二次函数关系,t与h的几组对应值如下表所示:
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度.