Question

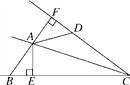
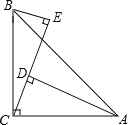
【题目】如图，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别为D，E．

（1）证明：△BCE≌△CAD；

（2）若AD=15cm，BE=8cm，求DE的长．

Answer 1

【答案】（1）见解析；（2）7cm．

【解析】

（1）根据垂直定义求出∠BEC=∠ACB=∠ADC，根据同角的余角相等得出∠ACD=∠CBE，根据AAS证明△CAD≌△BCE；

（2）根据全等三角形的对应边相等得到AD=CE，BE=CD，利用DE=CE﹣CD，即可得出结论．

（1）∵∠ACB=90°，BE⊥CE，AD⊥CE，

∴∠BEC=∠ACB=∠ADC=90°，

∴∠ACE+∠BCE=90°，∠BCE+∠CBE=90°，

∴∠ACD=∠CBE．

在△CAD和△BCE中，

∵，

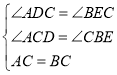∴△CAD≌△BCE；

（2）∵△CAD≌△BCE，

∴AD=CE，BE=CD，

∴DE=CE﹣CD=AD﹣BE=15﹣8=7(cm)．