题目内容
【题目】如图1,在Rt△ACB中,∠ACB=90°,∠ABC=30°,AC=1,点D为AC上一动点,连接BD,以BD为边作等边△BDE,设CD=n. 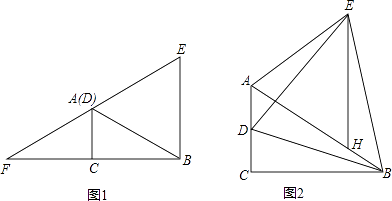
(1)当n=1时,EA的延长线交BC的延长线于F,则AF=;
(2)当0<n<1时,如图2,在BA上截取BH=AD,连接EH.
①设∠CBD=x,用含x的式子表示∠ADE和∠ABE.
②求证:△AEH为等边三角形.
【答案】
(1)2
(2)解:①证明:∵△BDE是等边三角形,
∴BE=BD,∠EDB=∠EBD=60°,
在△BCD中,∠ADE+∠EDB=∠CBD+∠C,
即∠ADE+60°=∠CBD+90°=x+90°,
∴∠ADE=30°+∠CBD,
∵∠HBE+∠ABD=60°,∠CBD+∠ABD=30°,
∴∠HBE=30°+∠CBD,
∴∠ADE=∠HBE,
∴∠ABE=∠ADE=x+90°;
②在△ADE与△HBE中,
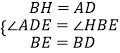 ,
,
∴△ADE≌△HBE(SAS),
∴AE=HE,∠AED=∠HEB,
∴∠AED+∠DEH=∠DEH+∠HEB,
即∠AEH=∠BED=60°,
∴△AEH为等边三角形
【解析】(1)解:∵△BDE是等边三角形,
∴∠EDB=60°,
∵∠ACB=90°,∠ABC=30°,
∴∠BAC=180°﹣90°﹣30°=60°,
∴FAC=180°﹣60°﹣60°=60°,
∴∠F=180°﹣90°﹣60°=30°,
∵∠ACB=90°,
∴∠ACF=180°﹣90°,
∴AF=2AC=2×1=2;
故答案为:2.
(1)根据三角形内角和定理求出∠BAC=60°,再根据平角等于180°求出∠FAC=60°,然后求出∠F=30°,根据30°角所对的直角边等于斜边的一半求解即可;(2)①根据三角形的任意一个外角等于与它不相邻的两个内角的和利用∠CBD表示出∠ADE=30°+∠CBD,又∠HBE=30°+∠CBD,从而得到∠ADE=∠ABE;②然后根据边角边证明△ADE与△HBE全等,根据全等三角形对应边相等可得AE=HE,对应角相等可得∠AED=∠HEB,然后推出∠AEH=∠BED=60°,再根据等边三角形的判定即可证明.

 阅读快车系列答案
阅读快车系列答案

