题目内容
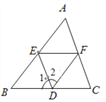
【题目】如图,在等边三角形ABC中,点E、D分别从A、C出发,沿AC,CB方向以相同的速度在线段AC,CB上运动,AD、BE相交于F点. 
(1)求证:△ABE≌△CAD;
(2)当E、D运动时,∠BFD大小是否发生改变?若不变求其大小,若改变求其变化范围.
【答案】
(1)解:∵△ABC是等边三角形,
∴AC=AB,∠C=∠BAE=60°,
∵点E、D分别从A、C出发,沿AC,CB方向以相同的速度在线段AC,CB上运动,
∴BD=CE,
∴AE=CD,
在△ABE和△CAD中,
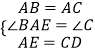 ,
,
∴△ABE≌△CAD
(2)解:当E、D运动时,∠BFD大小不发生改变,
∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∵∠AFE=∠ABE+∠BAF,
∴∠AFE=∠CAD+∠BAF=∠BAC=60°,
∵∠AFE=∠BFD(对顶角相等),
∴∠BFD=60°
【解析】(1)由等边三角形ABC可得出的条件是:AB=AC,∠BAC=∠ACB=60°,可根据SAS证明△ABE≌△CAD;(2)E、D运动时,∠BFD大小不发生改变,根据△ABE≌△CAD,得到∠ABE=∠CAD,利用外角的性质得到∠AFE=∠ABE+∠BAF,再根据对顶角相等,即可解答.
【考点精析】根据题目的已知条件,利用等边三角形的性质的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
相关题目