题目内容
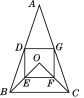
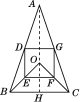
【题目】如图,在△ABC中,AB=AC,点O在△ABC的内部,∠BOC=90°,OB=OC,D,E,F,G分别是AB,OB,OC,AC的中点.
(1)求证:四边形DEFG是矩形;
(2)若DE=2,EF=3,求△ABC的面积.
【答案】(1)证明见解析 (2)21
【解析】
(1)连接AO并延长交BC于H,首先四边形DEFG是平行四边形,然后证得EF⊥DE,从而证得平行四边形DEFG是矩形;
(2)根据△BOC是等腰直角三角形,求得BC和AH的长,利用三角形的面积计算公式求其面积即可.
(1)证明:如图,连接AO并延长交BC于H,
∵AB=AC,OB=OC,
∴AH是BC的中垂线,即AH⊥BC.
∵D,E,F,G分别是AB,OB,OC,AC的中点,
(第14题)
∴DG∥EF∥BC,DE∥AH∥GF.
∴四边形DEFG是平行四边形.
∵EF∥BC,
AH⊥BC,
∴AH⊥EF.
又∵DE∥AH,
∴EF⊥DE,
∴四边形DEFG是矩形.
(2)解:∵D,E,F分别是AB,OB,OC的中点,
∴AO=2DE=4,BC=2EF=6.
∵△BOC是等腰直角三角形,
∴OH=![]() BC=3.
BC=3.
∴AH=OA+OH=4+3=7.
∴S△ABC=![]() ×6×7=21.
×6×7=21.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某学校为了了解九年级女生仰卧起坐训练情况,课外活动时间随机抽取10名女生测试,成绩如下表所示,那么这10名女生测试成绩的众数与中位数依次是( )
女生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩/个 | 48 | 49 | 52 | 47 | 51 | 53 | 52 | 49 | 51 | 49 |
A.52,51
B.51,51
C.49,49
D.49,50