题目内容
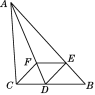
【题目】如图，在△ABC中，∠BAC的平分线交BC于点D，E是AB上一点，且AE＝AC，EF∥BC交AD于点F.
求证：四边形CDEF是菱形．
【答案】证明见解析
【解析】
根据AE＝AC，得出△ACE为等腰三角形，根据AD是∠BAC的平分线得出AO⊥CE，且OC＝OE. 由EF∥CD得出∠OEF＝∠OCD，再根据ASA证明△DOC≌△FOE，
得出OD＝OF，直接由菱形的判定可知四边形CDEF是菱形．
证明：如图，连接CE，交AD于点O.
∵AC＝AE，
∴△ACE为等腰三角形．
∵AO平分∠CAE，
∴AO⊥CE，且OC＝OE.
∵EF∥CD，
∴∠OEF＝∠OCD.
又∵∠DOC＝∠FOE，
∴△DOC≌△FOE(ASA)．
∴OD＝OF.
即CE与DF互相垂直且平分，
∴四边形CDEF是菱形．
练习册系列答案
阅读快车系列答案
相关题目
【题目】
市首批一次性投放公共自行车700辆供市民租用出行，由于投入数量不够， 导致出现需要租用却未租到车的现象，现随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
时间 | 第一天7：00﹣8：00 | 第二天7：00﹣8：00 | 第三天7：00﹣8：00 | 第四天7：00﹣8：00 | 第五天7：00﹣8：00 |
需要租用自行车却未租到车的人数（人） | 1500 | 1200 | 1300 | 1300 | 1200 |
（1）表格中的五个数据（人数）的中位数是多少？
（2）由随机抽样估计，平均每天在7:00-8:00 :需要租用公共自行车的人数是多少？
