题目内容
【题目】抛物线y＝﹣x2+x+b与x轴交于A、B两点，与y轴交于点C．
（1）若B点坐标为（2，0）
①求实数b的值；
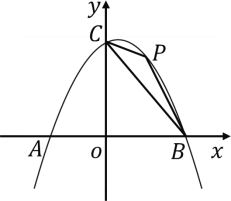
②如图1，点E是抛物线在第一象限内的图象上的点，求△CBE面积的最大值及此时点E的坐标．
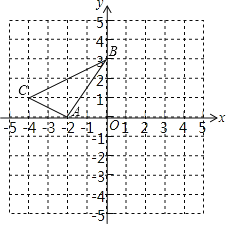
（2）如图2，抛物线的对称轴交x轴于点D，若抛物线上存在点P，使得P、B、C、D四点能构成平行四边形，求实数b的值．（提示：若点M，N的坐标为M（x，y），N（x，y），则线段MN的中点坐标为（
，
）
【答案】（1）①b＝2；②△CBE面积的最大值为1，此时E（1，2）；（2）b＝﹣1+
或b＝
，（
，
）
【解析】
（1）①将点B（2，0）代入y＝﹣x2+x+b即可求b；
②设E（m，﹣m2+m+2），求出BC的直线解析式为y＝﹣x+2，和过点E与BC垂直的直线解析式为y＝x﹣m2+2，求出两直线交点F，则EF最大时，△CBE面积的最大；
（2）可求C（0，b），B（
，0），设M（t，﹣t2+t+b），利用对角线互相平分的四边形是平行四边形，则分三种情况求解：①当CM和BD为平行四边形的对角线时，
＝
，
＝0，解得b＝﹣1+；②当BM和CD为平行四边形的对角线时，
＝
，＝
，b无解；③当BC和MD为平行四边形的对角线时，
＝，＝，解得b＝或b＝﹣（舍）．
解：（1）①将点B（2，0）代入y＝﹣x2+x+b，
得到0＝﹣4+2+b，
∴b＝2；
②C（0，2），B（2，0），
∴BC的直线解析式为y＝﹣x+2，
设E（m，﹣m2+m+2），
过点E与BC垂直的直线解析式为y＝x﹣m2+2，
∴直线BC与其垂线的交点为F（
，﹣+2），
∴EF＝
（﹣+2）＝[﹣
（m﹣1）2+]，
当m＝1时，EF有最大值
，
∴S＝×BC×EF＝×2×＝1，
∴△CBE面积的最大值为1，此时E（1，2）；
（2）∵抛物线的对称轴为x＝，
∴D（，0），
∵函数与x轴有两个交点，
∴△＝1+4b＞0，
∴b＞﹣，
∵C（0，b），B（，0），
设M（t，﹣t2+t+b），
①当CM和BD为平行四边形的对角线时，
C、M的中点为（，），B、D的中点为（，0），
∴＝，＝0，
解得：b＝﹣1+或b＝﹣1﹣（舍去），
∴b＝﹣1+；
②当BM和CD为平行四边形的对角线时，
B、M的中点为（，），C、D的中点为（，），
∴＝，＝，
∴b无解；
③当BC和MD为平行四边形的对角线时，
B、C的中点为（，），M、D的中点为（，），
∴＝，＝，
解得：b＝或b＝﹣（舍）；
综上所述：b＝﹣1+ 或b＝．
