题目内容
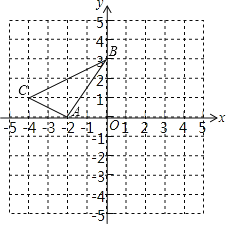
【题目】如图，在平面直角坐标系xOy中，A（﹣2，0），B（0，3），C（﹣4，1）．以原点O为旋转中心，将△ABC顺时针旋转90°得到△A'B'C'，其中点A，B，C旋转后的对应点分别为点A'，B'，C'．
（1）画出△A'B'C'，并写出点A'，B'，C'的坐标；
（2）求经过点B'，B，A三点的抛物线对应的函数解析式．
【答案】（1）见解析；（2）抛物线的解析式为y＝﹣
x2+x+3．
【解析】
（1）分别作出A，B，C的对应点A′，B′，C′即可．
（2）设抛物线的解析式为y＝a（x+2）（x﹣3），把B（0，3）代入求出a即可．
解：（1）如图△A'B'C'即为所求．A′（0，2），B′（3，0），C′（1，4）
（2）设抛物线的解析式为y＝a（x+2）（x﹣3），
把B（0，3）代入得到a＝﹣，
∴抛物线的解析式为y＝﹣x2+x+3．
练习册系列答案
相关题目
【题目】小明经过市场调查，整理出他妈妈商店里一种商品在第
天的销售量的相关信息如下表：
时间第 |
|
|
售价（元/件） |
| 50 |
每天销量（件） |
| |
已知该商品的进价为每件20元，设销售该商品的每天利润为
元.
（1）求出与
的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于2400元？请直接写出结果.
