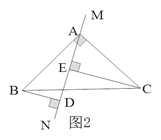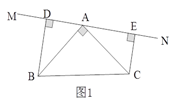题目内容
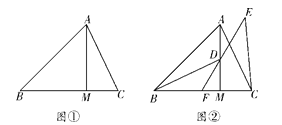
【题目】在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.
(1)如图①,若AB=3![]() ,BC=5,求AC的长;
,BC=5,求AC的长;
(2)如图②,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)先由AM=BM=ABcos45°=3可得CM=2,再由勾股定理可求出AC的长;
(2)延长EF到点G,使得FG=EF,证ΔBMD≌ΔANC得AC=BD,再证ΔBFG≌ΔCFE得BG=CE,∠G=∠E,从而得BD=BG=CE,即可得∠BDG=∠G=∠E.
试题解析:(1)∵∠ABM=45°,AM⊥BM,
∴AM=BM=ABcos45°=3![]() ×
×![]() =3,
=3,
则CM=BC﹣BM=5﹣2=2,
∴AC=![]() ;
;
(2)延长EF到点G,使得FG=EF,连接BG.

由DM=MC,∠BMD=∠AMC,BM=AM,
∴△BMD≌△AMC(SAS),
∴AC=BD,
又CE=AC,
因此BD=CE,
由BF=FC,∠BFG=∠EFC,FG=FE,
∴△BFG≌△CFE,
故BG=CE,∠G=∠E,
所以BD=BG=CE,
因此∠BDG=∠G=∠E.
考点:1.全等三角形的判定与性质;2.勾股定理.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目