题目内容
已知:AB是⊙O的弦,OD⊥AB于M交⊙O于点D,CB⊥AB交AD的延长线于C.
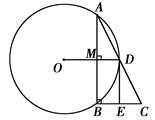
(1)求证:AD=DC;
(2)过D作⊙O的切线交BC于E,若DE=2,CE=1,求⊙O的半径.

(1)求证:AD=DC;
(2)过D作⊙O的切线交BC于E,若DE=2,CE=1,求⊙O的半径.
(1)证明:在⊙O中,OD⊥AB,CB⊥AB,
∴AM=MB,OD∥BC. …………………1分
…………………1分
∴AD=DC. ……………2分
……………2分
(2)∵DE为⊙O切线,
∴OD⊥DE ……………3分
∴四边形MBED为矩形.
∴DE∥AB. ……………4分
∴MB=DE=2,MD=BE=EC=1.
连接OB.
在Rt△OBM中,OB2="OM2+BM2. "
解得 OB= . …………………5分
. …………………5分
∴AM=MB,OD∥BC.
 …………………1分
…………………1分∴AD=DC.
 ……………2分
……………2分(2)∵DE为⊙O切线,
∴OD⊥DE ……………3分
∴四边形MBED为矩形.
∴DE∥AB. ……………4分
∴MB=DE=2,MD=BE=EC=1.
连接OB.
在Rt△OBM中,OB2="OM2+BM2. "
解得 OB=
 . …………………5分
. …………………5分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

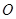 的直径
的直径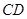 过弦
过弦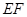 的中点
的中点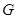 ,∠
,∠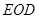 =
=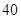 °,则∠
°,则∠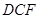 等于
等于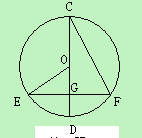
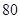 °
°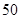 °
°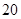 °
°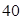 °
°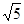 ,tan∠BOC=
,tan∠BOC= ,则OA′=
,则OA′= 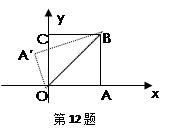
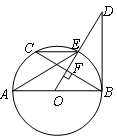
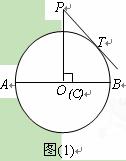
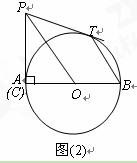
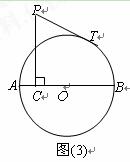
 置关系,并给出证明;
置关系,并给出证明;

 到A点时,连结PO、BT,求证:PO∥BT;
到A点时,连结PO、BT,求证:PO∥BT;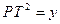 ,
,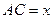 ,求
,求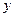 与
与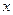 的函数关系式及
的函数关系式及