题目内容
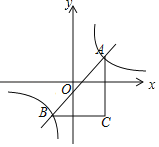
【题目】如图，直线y=x+m与双曲线y=
相交于A，B两点，BC∥x轴，AC∥y轴，则△ABC面积的最小值为_____．
【答案】6
【解析】
根据双曲线y=
过A，B两点，可设A（a，
），B（b，
），则C（a，）．将y=x+m代入y=，整理得x2+mx-3=0，由于直线y=x+m与双曲线y=相交于A，B两点，所以a、b是方程x2+mx-3=0的两个根，根据根与系数的关系得出a+b=-m，ab=-3，那么（a-b）2=（a+b）2-4ab=m2+12．再根据三角形的面积公式得出S△ABC=
ACBC=m2+6，利用二次函数的性质即可求出当m=0时，△ABC的面积有最小值6．
设A（a，），B（b，），则C（a，）．
将y=x+m代入y=，得x+m=，
整理，得x2+mx-3=0，
则a+b=-m，ab=-3，
∴（a-b）2=（a+b）2-4ab=m2+12．
∵S△ABC=ACBC
=（-）（a-b）
=
（a-b）
=（a-b）2
=（m2+12）
=m2+6，
∴当m=0时，△ABC的面积有最小值6．
故答案为6．
练习册系列答案
相关题目
【题目】中秋节前夕，某超市采购了一批土特产，根据以往销售经验，每天的售价与销售量之间有如下表的关系：
每千克售价(元) | 38 | 37 | 36 | 35 | … | 20 |
每天销售量(千克) | 50 | 52 | 54 | 56 | … | 86 |
设当售价从38元/千克下调到x元/千克时，销售量为y千克．
(1)根据上述表格中提供的数据，通过在直角坐标系中描点连线等方法，猜测并求出y与x之间的函数解析式；
(2)如果这种土特产的成本价是20元/千克，为使某一天的利润为780元，那么这一天每千克的售价应为多少元？(利润＝销售总金额－成本)
