题目内容
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(﹣ ![]() ,3),反比例函数y=
,3),反比例函数y= ![]() 的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( ) 
A.4 ![]()
B.﹣4 ![]()
C.2 ![]()
D.﹣2 ![]()
【答案】B
【解析】解:延长AC交y轴于E,如图, 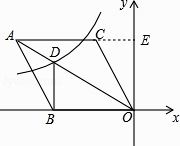
∵菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,
∴AC∥OB,
∴AE⊥y轴,
∵C(﹣ ![]() ,3),
,3),
∴OC= ![]() =2
=2 ![]() ,∠EOC=30°,
,∠EOC=30°,
∴∠BOC=60°,
∵四边形OBAC为菱形,
∴∠AOB=∠AOC,OB=OC=2 ![]() ,AC∥OB,
,AC∥OB,
∴∠COE=30°,
在Rt△BDO中,
∵BD= ![]() OB=2,
OB=2,
∴D点坐标为(﹣2 ![]() ,2),
,2),
∵反比例函数y= ![]() 的图象经过点D,
的图象经过点D,
∴k=﹣2 ![]() ×2=﹣4
×2=﹣4 ![]() ,
,
故选B.
延长AC交y轴于E,由已知得到∠COE=30°,OC=2 ![]() 如图,根据菱形的性质得AC∥OB,则AE⊥y轴,接着根据菱形的性质得OB=OC=2
如图,根据菱形的性质得AC∥OB,则AE⊥y轴,接着根据菱形的性质得OB=OC=2 ![]() ,∠BOA=30°,于是在Rt△BDO中可计算出BD=2,所以D点坐标为(﹣2
,∠BOA=30°,于是在Rt△BDO中可计算出BD=2,所以D点坐标为(﹣2 ![]() ,2),然后利用反比例函数图象上点的坐标特征可求出k的值.
,2),然后利用反比例函数图象上点的坐标特征可求出k的值.

练习册系列答案
相关题目