题目内容
【题目】定义：如果一个 
与 
的函数图像经过平移后能与某反比例函数的图像重合，那么称这个函数是 与 的“反比例平移函数”．
例如: 
的图像向左平移2个单位，再向下平移1个单位得到 
的图像，则 是 与 的“反比例平移函数”．
（1）若矩形的两边分别是2cm、3cm，当这两边分别增加 cm、 cm后，得到的新矩形的面积为8 
，求 与 的函数表达式，并判断这个函数是否为“反比例平移函数”．
（2）如图，在平面直角坐标系中，点O为原点，矩形OABC的顶点A、C的坐标分别为(9，0)、(0，3) ．点D是OA的中点，连接OB、CD交于点E，“反比例平移函数” 
的图像经过B、E两点．则这个“反比例平移函数”的表达式为；这个“反比例平移函数”的图像经过适当的变换与某一个反比例函数的图像重合，请写出这个反比例函数的表达式 ． 
（3）在（2）的条件下， 已知过线段BE中点的一条直线 
交这个“反比例平移函数”图像于P、Q两点(P在Q的右侧)，若B、E、P、Q为顶点组成的四边形面积为16，请求出点P的坐标．
【答案】
（1）
解： 
，
∴ 
向右平移2个单位，再向上平移3个单位得到 
．
∴ 是“反比例平移函数”．
（2）
；
（3）
解：如图，
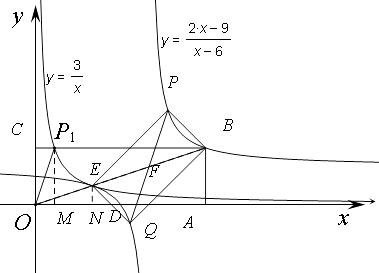
当点 
在点 
左侧时，设线段 
的中点为 
，由反比例函数中心对称性，四边形 
为平行四边形，
由B（9,3）得直线OB为y= 
x.
由D（3,0）,C(0，3)，设直线CD的解析式为y=mx+n,
则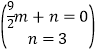
解得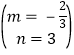
，
所以直线CD的解析式为y=
x+3.
联立
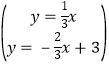解得
所以E（3,1）.
则F（
），即（6,2）.
∵四边形 的面积为16，
∴ 
=4，
∵ B (9,3)， F (6,2)，E (3，1)
是 的 “反比例平移函数”，
∴ 点B平移后与E重合，点F平移后与点O重合，点P平移后与点P1重合，
∴
= 
=4，
过 P1，E分别作 
轴的垂线，与 分别交于 
、 
点.
=
+ 
- 
=S梯形MNE
设 
，
∴ 
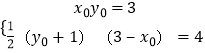
即 
∴ 
.
∴ 
(1，3)，∴点 的坐标为（7，5）.
当点 在点 右侧时，同理可得点 的坐标为（15， 
）.
【解析】解：（2）由A、C的坐标分别为(9，0)、(0，3)，可得B（9,3）
因为D是OA的中点，则D（
,0），
由B（9,3）和D（3,0）代入y=
， 得
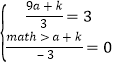解得
则y=
，
由图像y==
向左平移6个单位长度，再向下平移2个单位长度得y=
.
所以答案是y=；y=.
【考点精析】根据题目的已知条件，利用反比例函数的图象和反比例函数的性质的相关知识可以得到问题的答案，需要掌握反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点；性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大．
