题目内容
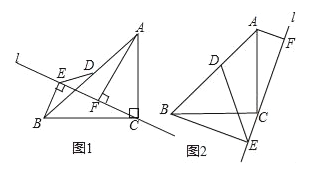
【题目】如图1,△ABC中,CA=CB,∠ACB=90°,直线l经过点C,AF⊥l于点F,BE⊥l于点E.
(1)求证:△ACF≌△CBE;
(2)将直线旋转到如图2所示位置,点D是AB的中点,连接DE.若AB=![]() ,∠CBE=30°,求DE的长.
,∠CBE=30°,求DE的长.
【答案】(1)答案见解析;(2)![]()
【解析】试题分析:(1)根据垂直的定义得到∠BEC=∠ACB=90°,根据全等三角形的性质得到∠EBC=∠CAF,即可得到结论;
(2)连接CD,DF,证得△BCE≌△ACF,根据全等三角形的性质得到BE=CF,CE=AF,证得△DEF是等腰直角三角形,根据等腰直角三角形的性质得到EF=![]() DE,EF=CE+BE,进而得到DE的长.
DE,EF=CE+BE,进而得到DE的长.
试题解析:解:(1)∵BE⊥CE,∴∠BEC=∠ACB=90°,∴∠EBC+∠BCE=∠BCE+∠ACF=90°,∴∠EBC=∠CAF.∵AF⊥l于点F,∴∠AFC=90°.
在△BCE与△ACF中,∵ ,∴△ACF≌△CBE(AAS);
,∴△ACF≌△CBE(AAS);
(2)如图2,连接CD,DF.∵BE⊥CE,∴∠BEC=∠ACB=90°,∴∠EBC+∠BCE=∠BCE+∠ACF=90°,∴∠EBC=∠CAF.∵AF⊥l于点F,∴∠AFC=90°.
在△BCE与△CAF中,∵ ,∴△BCE≌△CAF(AAS);
,∴△BCE≌△CAF(AAS);
∴BE=CF.∵点D是AB的中点,∴CD=BD,∠CDB=90°,∴∠CBD=∠ACD=45°,而∠EBC=∠CAF,∴∠EBD=∠DCF.在△BDE与△CDF中,∵ ,∴△BDE≌△CDF(SAS),∴∠EDB=∠FDC,DE=DF.∵∠BDE+∠CDE=90°,∴∠FDC+∠CDE=90°,即∠EDF=90°,∴△EDF是等腰直角三角形,∴EF=
,∴△BDE≌△CDF(SAS),∴∠EDB=∠FDC,DE=DF.∵∠BDE+∠CDE=90°,∴∠FDC+∠CDE=90°,即∠EDF=90°,∴△EDF是等腰直角三角形,∴EF=![]() DE,∴EF=CE+CF=CE+BE.∵CA=CB,∠ACB=90°,AB=4
DE,∴EF=CE+CF=CE+BE.∵CA=CB,∠ACB=90°,AB=4![]() ,∴BC=4.又∵∠CBE=30°,∴CE=
,∴BC=4.又∵∠CBE=30°,∴CE=![]() BC=2,BE=
BC=2,BE=![]() CE=2
CE=2![]() ,∴EF=CE+BE=2+2
,∴EF=CE+BE=2+2![]() ,∴DE=
,∴DE=![]() =
=![]() =
=![]() +
+![]() .
.


 名校课堂系列答案
名校课堂系列答案【题目】体育课上,甲、乙两个小组进行定点投篮对抗赛,每组10人,每人投10次.下表是甲组成绩统计表:
投进个数 | 10个 | 8个 | 6个 | 4个 |
人数 | 1个 | 5人 | 2人 | 2人 |
(1)请计算甲组平均每人投进个数;
(2)经统计,两组平均每人投进个数相同且乙组成的方差为3.2.若从成绩稳定性角度看,哪一组表现更好?