��Ŀ����
����Ŀ�����Գ������۲�����豭�����ÿֻ����20Ԫ���豭ÿֻ4Ԫ��������˫ʮһ���ڼ䳬�н���չ���������˿��ṩ�����Żݷ���:
����һ��ÿ��һֻ�������һֻ�豭��
������������Ͳ豭�������۵�90%���
ij�˿ͼƻ����ó��й�����5ֻ�Ͳ豭![]() ֻ���豭������5ֻ��.
ֻ���豭������5ֻ��.
��1���ú�![]() �Ĵ���ʽ�ֱ��ʾ����һ�뷽�������踶�����Ԫ��
�Ĵ���ʽ�ֱ��ʾ����һ�뷽�������踶�����Ԫ��
��2����![]() ʱ����ͨ������˵���ù˿�ѡ����������ֹ������ָ�ʡǮ��
ʱ����ͨ������˵���ù˿�ѡ����������ֹ������ָ�ʡǮ��
��3����![]() ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����
ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����
���𰸡�(1) ��1������һ�踶�4x��80��Ԫ���������踶�3.6x��90��Ԫ��(2)����һʡǮ��(3)��������
��������
(1)���������Żݷ����ֱ��г�����ʽ���ɣ�
(2)�ֱ����![]() ���м��㣬�ٱȽϼ��ɣ�
���м��㣬�ٱȽϼ��ɣ�
(3)�����ַ���������Ϲ��ɣ�
�⣺��1���˿Ͱ�����һ��������Ҫ����5��20��4��x5������4x��80��Ԫ��
�˿Ͱ���������������Ҫ����5��20��0.9��4��0.9x����3.6x��90��Ԫ��
��2����x��20Ԫʱ��
����һ�踶�4x��80��4��20��80��160��Ԫ����
�������踶�3.6x��90��3.6��20��90��162��Ԫ����
160��162��
��ѡ��һ�����ʡǮ��
��3���Ȱ�����һ����5�Ѳ��������5���豭������100Ԫ���ٰ�����������15���豭����15��4��0.9��54��Ԫ��������154Ԫ��
�˷����ȷ���һ��������ʡǮ��

����Ŀ����ͼ��Rt��ABC����C=90�㣬CA=CB=4![]() cm����PΪAB���ϵ�һ�����㣬��E��CA�ߵ��е�, ����PE����A��P�����ľ���Ϊxcm��P��E�����ľ���Ϊy cm.С������ѧϰ�����ľ��飬�Ժ���
cm����PΪAB���ϵ�һ�����㣬��E��CA�ߵ��е�, ����PE����A��P�����ľ���Ϊxcm��P��E�����ľ���Ϊy cm.С������ѧϰ�����ľ��飬�Ժ���![]() ���Ա���
���Ա���![]() �ı仯���仯�Ĺ��ɽ�����̽����
�ı仯���仯�Ĺ��ɽ�����̽����
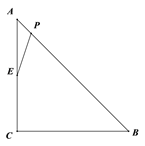
������С����̽�����̣��벹��������
��1��ͨ��ȡ�㡢��ͼ���������õ���![]() ��
��![]() �ļ���ֵ�����±���
�ļ���ֵ�����±���
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 2.8 | 2.2 | 2.0 | 2.2 | 2.8 | 3.6 | 5.4 | 6.3 |
��˵������ȫ����ʱ�����ֵ����һλС����
��2������ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��

��3����ϻ����ĺ���ͼ������⣺
��д���ú�����һ�����ʣ� ��
�ڵ�![]() ʱ��
ʱ��![]() �ij���ԼΪ cm.
�ij���ԼΪ cm.