��Ŀ����
����Ŀ�����壺�����������������![]() ������
������ ![]() ȡͬһ��ֵ��ʹ��
ȡͬһ��ֵ��ʹ��![]() ����ô��
����ô�� ![]() Ϊ��������ͨ���������ƶ�Ӧ��
Ϊ��������ͨ���������ƶ�Ӧ��![]() ֵΪ
ֵΪ![]() �������������� �����������������
�������������� �����������������![]() Ϊ��������ͨ����������ô
Ϊ��������ͨ����������ô![]() �����ֵ��Ϊ
�����ֵ��Ϊ![]() ������ֵͨ��.
������ֵͨ��.
��1���жϺ���![]() ��
��![]() �Ƿ�Ϊ����ͨ����������������ǣ������
�Ƿ�Ϊ����ͨ����������������ǣ������![]() ʱ���ǵ�������������������ǣ���˵�����ɣ�
ʱ���ǵ�������������������ǣ���˵�����ɣ�
��2����![]() ʱ����֪����
ʱ����֪����![]() ��
��![]() ����������ͨ������.����Ψһ������������
����������ͨ������.����Ψһ������������
�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�������ǵ�����ֵͨ��Ϊ18 ������� ![]() ��ֵ.
��ֵ.
���𰸡���1��![]() ��
��![]() �ǻ�����ͨ������������Ϊ
�ǻ�����ͨ������������Ϊ![]() ��
��![]() ����2������
����2������![]() ��
��![]() ʱ����
ʱ����![]() ��ֵΪ
��ֵΪ![]() ��3
��3
��������
(1)��������ʽ��ȥy���õ�����x�ķ��̣���������ʵ��������������Ϊ����������������m=2���뺯������������ʽ���x��ֵ��Ϊ�����㣻
(2)�ٵ�![]() ʱ�����m��ֵ����
ʱ�����m��ֵ����![]() ʱ�ǻ�����ͨ�������������x,y��ֵ�����ɽ��
ʱ�ǻ�����ͨ�������������x,y��ֵ�����ɽ��
�ڹ�Ӯ�㼴Ϊ![]() �����ֵ,��
�����ֵ,��![]() �Ƕ��κ����ҿ������ϣ��������ֵ�ڶ˵���ã��ֱ�
�Ƕ��κ����ҿ������ϣ��������ֵ�ڶ˵���ã��ֱ�![]() ��
��![]() �������ʽ������ֵ����18���õ�����m�ķ�����⼴�ɡ�
�������ʽ������ֵ����18���õ�����m�ķ�����⼴�ɡ�
��1��������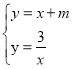
��![]()
��![]()
��![]() �������������
�������������
��![]() ��
��![]() Ϊ������ͨ����
Ϊ������ͨ����
��![]() ʱ��
ʱ��![]()
��![]()
�����Ϊ![]() ��
��![]()
��2���ٵ�![]() ʱ��
ʱ��
![]() ��
��![]()
�൱![]() ʱ�ǻ�����ͨ������
ʱ�ǻ�����ͨ������![]()
��������Ϊ![]()
��![]() ��
��![]() ʱ��������������ͨ������
ʱ��������������ͨ������
�������⣬
��![]()
��![]()
![]()
![]()
��![]() ��
��![]()
��![]() ��
��![]() ʱ��
ʱ��![]()
![]()
![]()
![]() ���ᣩ
���ᣩ
��![]() ʱ��
ʱ��![]()
![]() ���ᣩ
���ᣩ![]()
��![]() ��ֵΪ
��ֵΪ![]() ��3
��3

 Сѧ��ʱ��ҵȫͨ����ϵ�д�
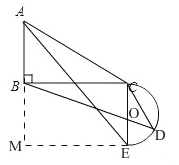
Сѧ��ʱ��ҵȫͨ����ϵ�д�����Ŀ����ͼ��Rt��ABC����C=90�㣬CA=CB=4![]() cm����PΪAB���ϵ�һ�����㣬��E��CA�ߵ��е�, ����PE����A��P�����ľ���Ϊxcm��P��E�����ľ���Ϊy cm.С������ѧϰ�����ľ��飬�Ժ���
cm����PΪAB���ϵ�һ�����㣬��E��CA�ߵ��е�, ����PE����A��P�����ľ���Ϊxcm��P��E�����ľ���Ϊy cm.С������ѧϰ�����ľ��飬�Ժ���![]() ���Ա���
���Ա���![]() �ı仯���仯�Ĺ��ɽ�����̽����
�ı仯���仯�Ĺ��ɽ�����̽����
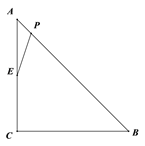
������С����̽�����̣��벹��������
��1��ͨ��ȡ�㡢��ͼ���������õ���![]() ��
��![]() �ļ���ֵ�����±���
�ļ���ֵ�����±���
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 2.8 | 2.2 | 2.0 | 2.2 | 2.8 | 3.6 | 5.4 | 6.3 |
��˵������ȫ����ʱ�����ֵ����һλС����
��2������ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��

��3����ϻ����ĺ���ͼ������⣺
��д���ú�����һ�����ʣ� ��
�ڵ�![]() ʱ��
ʱ��![]() �ij���ԼΪ cm.
�ij���ԼΪ cm.