��Ŀ����
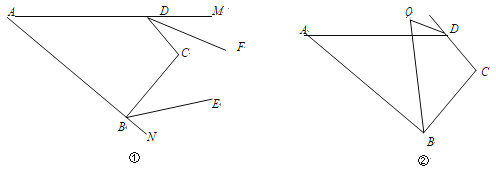
����Ŀ��������У�Ļ�У�ij��ȤС���������ͼ��ʾ��ֱ��ǽ�ǣ������㹻��������28m�������Χ��һ�����λ�ABCD�����ֻΧAB��BC���ߣ�����AB=xm��

��1�����������Ϊ192m2����x��ֵ��
��2������P����һ������ǽCD��AD�ľ���ֱ���15m��6m��Ҫ�������Χ�ڻ��ڣ����߽磬���������Ĵ�ϸ������xȡ��ֵʱ�������S�����������S�����ֵ��
���𰸡���1��x��ֵΪ12��16����2�������S�����ֵΪ195ƽ���ף�
�������������������1����������ó�������=192�������ó��𰸣�
��2��������ɵó���S=x��28-x��=-x2+28x=-��x-14��2+196�������ö��κ��������������ֵ��
�����������1����AB=x����BC=��28-x����
��x��28-x��=192��
��ã�x1=12��x2=16��
��x��ֵΪ12��16��
��2����AB=xm��
��BC=28-x��
��S=x��28-x��=-x2+28x=-��x-14��2+196��
����P����һ������ǽCD��AD�ľ���ֱ���15m��6m��
��28-15=13��
��6��x��13��
����x=13ʱ��Sȡ�����ֵΪ��S=-��13-14��2+196=195��
�𣺻����S�����ֵΪ195ƽ���ף�

����Ŀ���л�������ԴԶ�������л�ʫ�ʣ�Ԣ����㣮Ϊ�˴������㴫ͳ�Ļ�������ijУ��ί��֯��һ��ȫУ2000��ѧ���μӵ����й�ʫ�ʴ������ѡ���������������в���ѧ���ijɼ���������50�֣�Ϊ�˸��õ��˽Ȿ�κ�ѡ�����ijɼ��ֲ�����������ȡ������200��ѧ���ĺ�ѡ�����ɼ����ɼ�xȡ�������ܷ�100�֣���Ϊ���������������õ�����ͳ��ͼ��

��� | ��ѡ�ɼ�x |
A�� | 50��x��60 |
B�� | 60��x��70 |
C�� | 70��x��80 |
D�� | 80��x��90 |
E�� | 90��x��100 |
�����������Ϣ�������������
��ͼ1����ͳ��ͼ��D�������ж��٣�
����ͼ2������ͳ��ͼ�У��DZ�ʾB��������ռ�İٷֱ�Ϊa%����a��ֵΪ ����ʾC�����ε�Բ�ĽǵĶ���Ϊ �ȣ�
�۹涨��ѡ�ɼ���90�����ϣ�����90�֣���Ϊ���ŵ���������Ƹ�У�μ���κ�ѡ������2000��ѧ���гɼ����ŵ������ж����ˣ�
����Ŀ��������ġ�ˮ��Ⱦ���η�����2018��1��1����ʩ�У�ij��ҵΪ�������ˮ��������������������10̨��ˮ�����豸������![]() �����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±���
�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±���
|
| |
�۸���Ԫ/̨�� | 12 | 10 |
������ˮ������/�£� | 240 | 200 |
��Ԥ�㣬����ҵ�����豸���ʽ���105��Ԫ.
��1��������Ƹ���ҵ���ܵĹ�����
��2������ҵÿ�²�������ˮ��Ϊ2040�֣�Ϊ�˽�Լ�ʽ�Ӧѡ�����ֹ�������˵������.
����Ŀ�������±��еĶ��κ���y=ax2+bx+c���Ա���x�뺯��y�Ķ�Ӧֵ�����ж϶��κ����Ľ���ʽΪ��������
x | �� |
| 0 | 1 | 2 | �� |
y | �� |
|
|
|
| �� |
A. y=![]() x2��
x2��![]() x��
x��![]() B. y=
B. y=![]() x2+
x2+![]() x��
x��![]()
C. y=��![]() x2��
x2��![]() x+
x+![]() D. y=��
D. y=��![]() x2+
x2+![]() x+
x+![]()