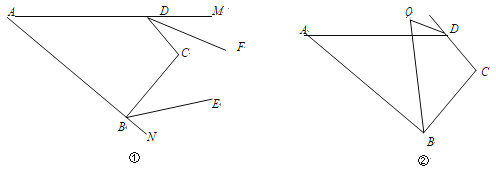
题目内容
【题目】如图,![]() ,
,![]() ,C、B、D在同一条直线上.
,C、B、D在同一条直线上.

(1)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
(2)如图设a、b、c是![]() 和
和![]() 的边长,这时我们把关于x的形如
的边长,这时我们把关于x的形如![]() 的一元二次方程称为“勾股方程”.
的一元二次方程称为“勾股方程”.
①写出一个“勾股方程”;
②判断关于x的“勾股方程”![]() 根的情况并说明理由;
根的情况并说明理由;
③若![]() 是“勾股方程”
是“勾股方程”![]() 的一个根,且四边形
的一个根,且四边形![]() 的周长是
的周长是![]() ,求
,求![]() 的面积.
的面积.

【答案】(1)![]() (2)①
(2)①![]() ②关于x的“勾股方程”
②关于x的“勾股方程”![]() 必有实数根,理由见解析.③
必有实数根,理由见解析.③![]()
【解析】
(1)由Rt△ABC≌Rt△BED,知BD=AC=1,DE=BC=![]() ∠ABC=∠BED,∠BAC=∠EBD,再证AB=BE=
∠ABC=∠BED,∠BAC=∠EBD,再证AB=BE=![]() ,∠ABE=90°,利用勾股定理可得答案;
,∠ABE=90°,利用勾股定理可得答案;
(2)①直接找一组勾股数代入方程即可;②通过判断根的判别式△的正负来证明结论;③利用根的意义和勾股定理作为相等关系先求得c的值,根据完全平方公式求得ab的值,从而可求得面积.
解:(1)∵Rt△ABC≌Rt△BED,
∴BD=AC=1,DE=BC=![]() ∠ABC=∠BED,∠BAC=∠EBD,
∠ABC=∠BED,∠BAC=∠EBD,
∴AB=BE=![]() ,
,
∵∠ABC+∠BAC=90°,
∴∠ABC+∠EBD=90°,
∴∠ABE=90°,
∴AE= ![]()
(2)①当a=3,b=4,c=5时,勾股方程为为![]()
②关于x的“勾股方程”![]() 必有实数根,
必有实数根,
理由如下:根据题意,得:![]()
∵![]()
∴![]()
即△≥0,
∴勾股方程![]() 必有实数根;
必有实数根;
③当![]() 时,有
时,有![]()
即![]()
∵四边形![]() 的周长是
的周长是![]() ,
,
![]()
![]() 即
即![]()
∴![]()
∴c=3,
∴![]()
![]()
∵![]()
![]()
∴![]()
∴![]() =
=![]()

【题目】中华文明,源远流长:中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表

组别 | 海选成绩x |
A组 | 50≤x<60 |
B组 | 60≤x<70 |
C组 | 70≤x<80 |
D组 | 80≤x<90 |
E组 | 90≤x<100 |
请根据所给信息,解答下列问题
①图1条形统计图中D组人数有多少?
②在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 ,表示C组扇形的圆心角的度数为 度;
③规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
【题目】修正后的《水污染防治法》于2018年1月1日起施行,某企业为了提高污水处理的能力,决定购买10台污水处理设备,现有![]() 两种型号的设备,其中每台的价格、月处理污水量如下表:
两种型号的设备,其中每台的价格、月处理污水量如下表:
|
| |
价格(万元/台) | 12 | 10 |
处理污水量(吨/月) | 240 | 200 |
经预算,该企业购买设备的资金不高于105万元.
(1)请你设计该企业可能的购买方案;
(2)若企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案?请说明理由.
【题目】为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来, 制成如表:
汽车行驶时间 t(小时) | 0 | 1 | 2 | 3 | … |
油箱剩余油量 Q(升) | 100 | 94 | 88 | 82 | … |
(1)上表反映的两个变量中,自变量是 ,因变量是 ;
(2)根据上表可知,该车油箱的大小为 升,每小时耗油 升;
(3)请求出两个变量之间的关系式(用 t 来表示 Q).