题目内容
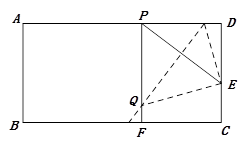
把矩形ABCD以对角线AC为折痕折叠(如图所示),设 AF交DC于点E。
求证:DE = FE
求证:DE = FE

证明见解析
证明:∵△ABC与△AFC关于AC对称,∴△ABC≌△AFC.
即,∠B=∠F,CF=BC=AD
在Rt△ADE与Rt△CFE中,∠AED=∠CEF(对顶角)
AD = CF (已证)
∠B=∠F (已证)
∴Rt△ADE≌Rt△CFE(AAS)
∴DE ="FE"
说明:本题有不同的证法,可参照评分.
根据对折的性质可以得到:△ABC≌△AFC,然后根据AAS即可证得:Rt△ADE≌Rt△CFE,从而证得DE=FE.
即,∠B=∠F,CF=BC=AD
在Rt△ADE与Rt△CFE中,∠AED=∠CEF(对顶角)
AD = CF (已证)
∠B=∠F (已证)
∴Rt△ADE≌Rt△CFE(AAS)
∴DE ="FE"
说明:本题有不同的证法,可参照评分.
根据对折的性质可以得到:△ABC≌△AFC,然后根据AAS即可证得:Rt△ADE≌Rt△CFE,从而证得DE=FE.

练习册系列答案
相关题目
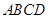 中,
中,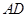 ∥
∥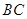 ,点
,点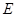 、
、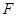 在边
在边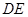 ∥
∥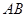 ,
, ∥
∥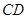 ,且四边形
,且四边形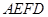 是平行四边形.
是平行四边形.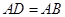 ;②∠
;②∠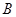 +∠
+∠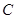 =90°;③∠
=90°;③∠
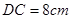 ,
, 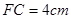 ,则
,则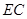 长为 ㎝.
长为 ㎝.
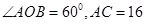 ,则图中长度为8的线段条数有( )
,则图中长度为8的线段条数有( )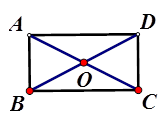
 ACF与
ACF与