题目内容
如图,平行四边形ABCD中,EF过AC的中点O,与边AD、BC分别相交于点E、F。
(1)试说明四边形AECF是平行四边形。
(2)若EF过AC的中点,且与AC垂直时,试说明四边形AECF是菱形。
(3)当EF与AC有怎样的数量和位置关系时,四边形AECF是矩形。

(1)试说明四边形AECF是平行四边形。
(2)若EF过AC的中点,且与AC垂直时,试说明四边形AECF是菱形。
(3)当EF与AC有怎样的数量和位置关系时,四边形AECF是矩形。

证明:
(1)在□ABCD中
AD∥BC
∴∠EAC =∠ACF ∠AEF =∠CFE
∵O是AC的中点
∴OA=OC
∴△AOE≌△COF
∴OE=OF
又∵OA=OC
∴四边形AECF是平行四边形
(2)由(1)可知四边形AECF是平行四边形
∵ EF⊥AC
∴ 四边形AECF是菱形
(3)当EF = AC时,四边形AECF是矩形。
理由:由(1)可知四边形AECF是平行四边形
∵EF = AC
∴ 四边形AECF是矩形
(1)在□ABCD中
AD∥BC
∴∠EAC =∠ACF ∠AEF =∠CFE
∵O是AC的中点
∴OA=OC
∴△AOE≌△COF
∴OE=OF
又∵OA=OC
∴四边形AECF是平行四边形
(2)由(1)可知四边形AECF是平行四边形
∵ EF⊥AC
∴ 四边形AECF是菱形
(3)当EF = AC时,四边形AECF是矩形。
理由:由(1)可知四边形AECF是平行四边形
∵EF = AC
∴ 四边形AECF是矩形
(1)根据平行四边形及O是AC的中点,推出△AOE≌△COF,即得OE=OF;
(2)根据对角线互相垂直的平行四边形是菱形推出即可;
(3)根据对角线相等的平行四边形是矩形推出即可.
(2)根据对角线互相垂直的平行四边形是菱形推出即可;
(3)根据对角线相等的平行四边形是矩形推出即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

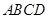 中,
中, ∥
∥ ,
, 平分
平分 ,
, 平分线交
平分线交 ,联结
,联结 .
.
 是菱形;
是菱形; 时,证明:梯形
时,证明:梯形

 ,那么AB=_________.
,那么AB=_________.

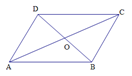
 中,对角线
中,对角线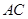 、
、 相交于点
相交于点 ,设
,设 ,
, ,那么
,那么 .
.
 ,使点
,使点 落在边
落在边 的点
的点 处,已知
处,已知
 ,求
,求 的长。
的长。