题目内容
已知:如图,在梯形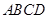 中,
中,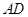 ∥
∥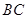 ,点
,点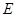 、
、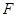 在边
在边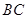 上,
上,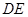 ∥
∥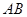 ,
,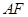 ∥
∥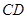 ,且四边形
,且四边形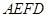 是平行四边形.
是平行四边形.
(1)试判断线段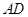 与
与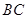 的长度之间有怎样的数量关系?并证明你的结论;
的长度之间有怎样的数量关系?并证明你的结论;
(2)现有三个论断:①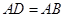 ;②∠
;②∠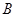 +∠
+∠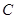 =90°;③∠
=90°;③∠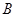 =2∠
=2∠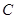 .请从上述三个论断中选择一个论断作为条件,证明四边形
.请从上述三个论断中选择一个论断作为条件,证明四边形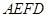 是菱形.
是菱形.
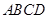 中,
中,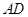 ∥
∥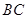 ,点
,点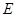 、
、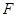 在边
在边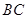 上,
上,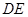 ∥
∥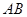 ,
,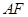 ∥
∥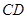 ,且四边形
,且四边形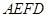 是平行四边形.
是平行四边形.(1)试判断线段
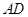 与
与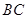 的长度之间有怎样的数量关系?并证明你的结论;
的长度之间有怎样的数量关系?并证明你的结论;(2)现有三个论断:①
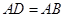 ;②∠
;②∠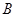 +∠
+∠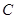 =90°;③∠
=90°;③∠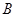 =2∠
=2∠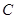 .请从上述三个论断中选择一个论断作为条件,证明四边形
.请从上述三个论断中选择一个论断作为条件,证明四边形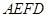 是菱形.
是菱形.
见解析
(1)线段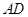 与
与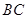 的长度之间的数量为:
的长度之间的数量为: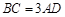 . (1分)
. (1分)
证明:∵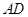 //
// 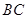 ,
,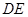 //
//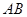 ,
,
∴四边形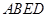 是平行四边形.
是平行四边形.
∴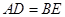 . (2分)
. (2分)
同理可证,四边形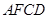 是平行四边形.即得
是平行四边形.即得 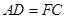 . (1分)
. (1分)
又∵ 四边形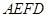 是平行四边形,∴
是平行四边形,∴ 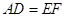 . (1分)
. (1分)
∴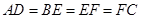 .
.
∴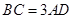 . (1分)
. (1分)
(2)选择论断②作为条件. (1分)
证明:∵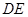 ∥
∥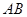 ,
,
∴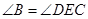 . (1分)
. (1分)
∵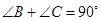 ,
,
∴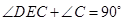 .
.
即得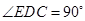 . (2分)
. (2分)
又∵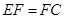 ,
,
∴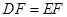 . (1分)
. (1分)
∵ 四边形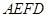 是平行四边形,
是平行四边形,
∴ 四边形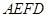 是菱形. (1分)
是菱形. (1分)
(1)由题中所给平行线,不难得出四边形ABED和四边形AFCD都是平行四边形,而四边形AEFD也是平行四边形,三个平行四边形都共有一条边AD,所以可得出BC=3AD的结论.
(2)可选择②作为证明条件,先证明DE=EF,然后结合四边形AEFD是平行四边形得出结论.
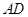 与
与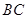 的长度之间的数量为:
的长度之间的数量为: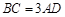 . (1分)
. (1分)证明:∵
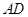 //
// 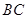 ,
,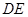 //
//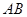 ,
,∴四边形
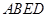 是平行四边形.
是平行四边形.∴
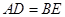 . (2分)
. (2分)同理可证,四边形
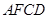 是平行四边形.即得
是平行四边形.即得 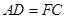 . (1分)
. (1分)又∵ 四边形
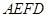 是平行四边形,∴
是平行四边形,∴ 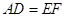 . (1分)
. (1分)∴
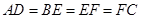 .
.∴
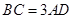 . (1分)
. (1分)(2)选择论断②作为条件. (1分)
证明:∵
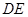 ∥
∥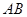 ,
,∴
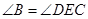 . (1分)
. (1分)∵
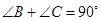 ,
,∴
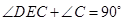 .
.即得
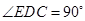 . (2分)
. (2分)又∵
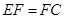 ,
,∴
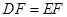 . (1分)
. (1分)∵ 四边形
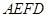 是平行四边形,
是平行四边形,∴ 四边形
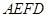 是菱形. (1分)
是菱形. (1分)(1)由题中所给平行线,不难得出四边形ABED和四边形AFCD都是平行四边形,而四边形AEFD也是平行四边形,三个平行四边形都共有一条边AD,所以可得出BC=3AD的结论.
(2)可选择②作为证明条件,先证明DE=EF,然后结合四边形AEFD是平行四边形得出结论.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目

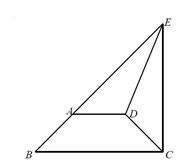
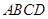 中,
中,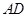 ∥
∥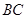 ,
,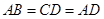 ,点
,点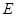 在
在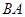 的延长线上,
的延长线上,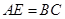 ,
,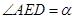 .
.
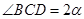 ;
;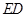 平分
平分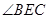 时,求证:△
时,求证:△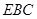 是等腰直角三角形.
是等腰直角三角形.
 中,对角线
中,对角线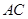 、
、 相交于点
相交于点 ,设
,设 ,
, ,那么
,那么 .
.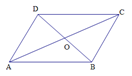


 ,使点
,使点 落在边
落在边 的点
的点 处,已知
处,已知
 ,求
,求 的长。
的长。
