题目内容
【题目】如图,在4×4正方形的网格中,线段AB,CD如图位置,每个小正方形的边长都是1.
(1)求出线段AB、CD的长度;
(2)在图中画出线段EF,使得EF=![]() ,并判断以AB,CD,EF三条线段组成的三角形的形状,请说明理由;
,并判断以AB,CD,EF三条线段组成的三角形的形状,请说明理由;
(3)我们把(2)中三条线段按照点E与点C重合,点F与点B重合,点D与点A重合,这样可以得△ABC,则点C到直线AB的距离为______(直接写结果).

【答案】(1)AB=![]() ,CD=
,CD=![]() ;(2)线段EF见解析,以AB,CD,EF三条线段组成的三角形是直角三角形,理由见解析;(3)
;(2)线段EF见解析,以AB,CD,EF三条线段组成的三角形是直角三角形,理由见解析;(3)![]() .
.
【解析】
(1)根据勾股定理计算即可解决问题;
(2)利用数形结合的思想解决问题,根据勾股定理的逆定理判断即可;
(3)利用面积法即可解决问题.
解:(1)AB=![]() ,CD=
,CD=![]() ;
;
(2)EF=![]() ,如图所示:
,如图所示: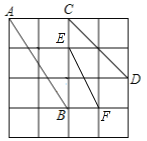
∵CD2+EF2=AB2
∴以AB,CD,EF三条线段组成的三角形是直角三角形;
(3)设C到直线AB的距离为h.
则有![]() ,
,
∴h=![]() ,
,
∴C到直线AB的距离为![]() .
.
故答案为(1)AB=![]() ,CD=
,CD=![]() ;(2)线段EF见解析,以AB,CD,EF三条线段组成的三角形是直角三角形,理由见解析;(3)
;(2)线段EF见解析,以AB,CD,EF三条线段组成的三角形是直角三角形,理由见解析;(3)![]() .
.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目