题目内容
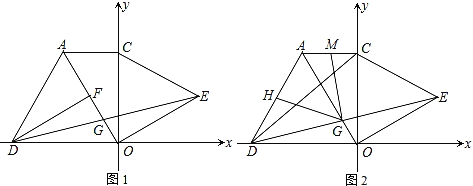
【题目】如图,在直角坐标系中,正方形OABC的顶点B的坐标为(3,3),直线CD交直线OA于点D,直线OE交线段AB于E,且CD⊥OE,垂直为点F,若图中阴影部分的面积是正方形OABC的面积的![]() ,则△OFC的周长为________.
,则△OFC的周长为________.

【答案】![]()
【解析】
先证明ΔCOD≌ΔOAE,推出ΔOCF的面积=四边形DAEF的面积,设OF=x,FC=y,由勾股定理和面积公式得出xy和![]() 的值,利用
的值,利用![]() 求出x+y值,即可得到周长.
求出x+y值,即可得到周长.
∵正方形OABC的顶点B的坐标为(3,3),
∴OC=OA=3,∠OAB=90,且正方形的面积为9,
∵阴影部分的面积是正方形OABC的面积的![]() ,
,
∴阴影的面积为9×![]() =3,
=3,
∵CD⊥OE,
∴∠AOE+∠ODC=90,
又∵∠OCD+∠ODC=90,
∴∠OCD=∠AOE,
在ΔCOD和ΔOAE中
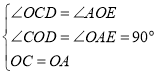
∴ΔCOD≌ΔOAE(AAS),
∴ΔOCF的面积=四边形DAEF的面积=3÷2=![]() ,
,
设设OF=x,FC=y,
则xy=3,![]() ,
,
∴![]() ,
,
∴![]() ,
,
所以△OFC的周长为![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】新华文具用品店最近购进了一批钢笔,进价为每支6元,为了合理定价,在销售前4天试行机动价格,卖出时每支以10元为标准,超过10元的部分记为正,不足10元的部分记为负。文具店记录了这四天该钢笔的售价情况和售出情况,如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
每支价格相对标准价格(元) | +1 | 0 | -1 | -2 |
售出支数(支) | 12 | 15 | 32 | 33 |
(1)填空:这四天中赚钱最多的是第______天,这天赚了______元钱;
(2)求新华文具用品店这四天出售这种钢笔一共赚了多少钱;
(3)新华文具用品店准备用这四天赚的钱全部购进这种钢笔,进价仍为每支6元为了促销这种钢笔,每只钢笔的售价在10元的基础上打九折,本次购进的这种钢笔全部售出后共赚了多少钱?