Question

【题目】（本题满分10分）如图，已知直线和双曲线 （k＞0），点A（m，n）在双曲线 上．当m=n=2时．

（1）直接写出k的值；

（2）将直线作怎样的平移能使平移后的直线与双曲线 只有一个交点．

Answer 1

【答案】（1）k=4；（2）向上或向下平移个单位长度．

【解析】试题分析：（1）当m=n=2时，得出A（2，2），把点A（2，2）代入双曲线 （k＞0）求出k的值即可；

（2）设平移后的直线解析式为y=﹣x+b1，由直线和双曲线解析式组成方程组，整理可得方程：x2﹣b1x+4=0，当判别式=0时，求出b1=±4即可．

试题解析：解：（1）当m=n=2时，A（2，2），把点A（2，2）代入双曲线（k＞0）得：k=2×2=4；

（2）设平移后的直线解析式为y=﹣x+b1，由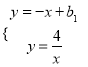 可得， ，整理可得：x2﹣b1x+4=0，当△=，即b1=±4时，方程x2﹣b1x+4=0有两个相等的实数根，此时直线y=﹣x+b1与双曲线只有一个交点，∴只要将直线y=﹣x向上或向下平移4个单位长度，所得到的直线与双曲线只有一个交点．