题目内容
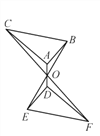
【题目】已知:如图,边长为2的正五边形ABCDE内接于⊙O,AB、DC的延长线交于点F,过点E作EG∥CB交BA的延长线于点G.

(1)求证: ![]() ;
;
(2)证明:EG与⊙O相切,并求AG、BF的长.
【答案】(1)见解析;(2)见解析
【解析】试题分析:欲证AB2=AGBF,可证△EAG∽△FBC及正五边形ABCDE的特点得出;求AG、BF的长,需连接EF,易证明EF⊥BC,得出EF⊥EG,依据EG与⊙O相切,用切线的性质得出.
试题解析:证明:(1)易证五边形ABCDE的外角∠FCB=∠EAG=∠FBC,
∵EG∥CB,
∴∠EAG=∠FBC.
∴△EAG∽△FBC.
∴![]() ,即BCAE=AGBF.
,即BCAE=AGBF.
又∵BC=AE=AB,
∴![]() .①
.①
(2)连接EF,由(1)可知FB=FC,即△FBC为等腰三角形,易知BA=CD,

∴FA=FD,
∴EF⊥BC且EF平分BC,
∴EF过圆心O.
又∵EG∥CB,∴EF⊥EG,
∴EG与⊙O相切.
∴![]() .
.
由(1)可知∠G=∠EAG,∴EG=EA=2,
设AG=x,则![]() ,解得
,解得![]()
∴AG=![]() ,代入①中可得:BF=
,代入①中可得:BF=![]() .
.

练习册系列答案
相关题目