题目内容
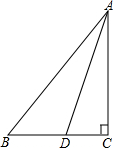
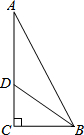
在数学活动课上,小明提出这样一个问题:如图,AB⊥BC,DC⊥BC,E是BC的中点,AB+CD=AD,DE平分∠ADC,∠CED=40°,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是______.


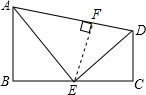
如图,过点E作EF⊥AD于F,
∵DE平分∠ADC,DC⊥BC,
∴CE=EF,
∵E是BC的中点,
∴CE=BE,
∴EF=BE,
又∵AB⊥BC
∴∠B=90°,
∴AE是∠BAD的平分线,
∴∠DAE+∠ADE=
(360°-90°×2)=90°,
∴∠AED=180°-90°=90°,
∵∠CED+∠AEB=180°-90°=90°,
∠EAB+∠AEB=90°,
∴∠EAB=∠CED=40°.
故答案为:40°.
∵DE平分∠ADC,DC⊥BC,
∴CE=EF,
∵E是BC的中点,
∴CE=BE,
∴EF=BE,
又∵AB⊥BC
∴∠B=90°,
∴AE是∠BAD的平分线,
∴∠DAE+∠ADE=
| 1 |
| 2 |
∴∠AED=180°-90°=90°,
∵∠CED+∠AEB=180°-90°=90°,
∠EAB+∠AEB=90°,
∴∠EAB=∠CED=40°.
故答案为:40°.


练习册系列答案
相关题目