Question

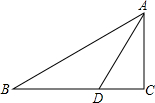
如图，已知，∠BAD=120°，AC平分∠BAD，若∠ABC+∠ADC=180°，则如下结论一定正确的有（　　）个
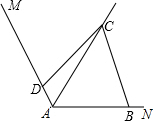
①DC=BC；②AD+AB=AC；③S_△ABC=3S_△ACD；④∠ACB=3∠ACD．

A．4

B．3

C．2

D．1

Answer 1

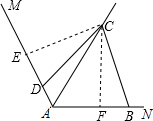
过C作CF⊥AB于F，CE⊥AM于E，
∵AC平分∠BAD，
∴CE=CF，∠CED=∠CFB=90°，
∵∠ABC+∠ADC=180°，∠ADC+∠EDC=180°，
∴∠CBF=∠EDC，
在△EDC和△FBC中，

∠CDE=∠CBF ∠CED=∠CFB CE=CF

，
∴△EDC≌△FBC（AAS），
∴CD=CB，DE=FB，
∵CE=CF，AC=AC，
∴由勾股定理得：AE=AF，
∵∠BAD=120°，AC平分∠BAD，
∴∠CAF=60°，
∴∠ACF=30°，
∵∠AFC=90°，
∴AC=2AF=AE+AF，
∵AD+AB=AD+AF+FB=AD+AF+DE=AE+AF=2AF，
∴AD+AB=AC，∴①正确；②正确；
当∠ABC=∠ADC=90°时，S_△ADC=S_△ABC，∠ACB=∠ACD，∴③④错误；
故选C．