题目内容
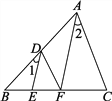
【题目】在ABCD中,点P和点Q是直线BD上不重合的两个动点,AP∥CQ,AD=BD.
(1)如图①,求证:BP+BQ=BC;
(2)请直接写出图②,图③中BP、BQ、BC三者之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,若DQ=1,DP=3,则BC=______.

【答案】(1)证明见解析;(2)图②:BQ﹣BP=BC, 图③:BP﹣BQ=BC;(3)BC=2或4.
【解析】分析:(1)根据平行四边形的性质证明△ADP≌△CBQ,得BQ=PD,由AD=BD=BC得:BC=BD=BP+PD=BP+BQ;(2)图②,证明△ABP≌△CDQ,得PB=DQ,根据线段的和得结论;图③,证明△ADP≌△CBQ,得PD=BQ,同理得出结论;(3)分别代入图①和图②条件下的BC,计算即可.
本题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∴∠ADB=∠CBD,
∵AP∥CQ,∴∠APQ=∠CQB,∴△ADP≌△CBQ, ∴DP=BQ,
∵AD=BD,AD=BC,∴BD=BC,∵BD=BP+DP,∴BC=BP+BQ;
(2)图②:BQ﹣BP=BC,理由是:
∵AP∥CQ,∴∠APB=∠CQD,
∵AB∥CD,∴∠ABD=∠CDB,
∴∠ABP=∠CDQ,∵AB=CD,
∴△ABP≌△CDQ,∴BP=DQ,
∴BC=AD=BD=BQ﹣DQ=BQ﹣BP;
图③:BP﹣BQ=BC,理由是:
同理得:△ADP≌△CBQ,
∴PD=BQ,
∴BC=AD=BD=BP﹣PD=BP﹣BQ;
(3)图①,BC=BP+BQ=DQ+PD=1+3=4,
图②,BC=BQ﹣BP=PD﹣DQ=3﹣1=2,
∴BC=2或4.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】为了解甲、乙两名运动员的体能训练情况,对他们进行了跟踪测试,并把连续十周的测试成绩绘制成如图所示的折线统计图.教练组规定:体能体能测试成绩70分以上(包括70分)为合适. 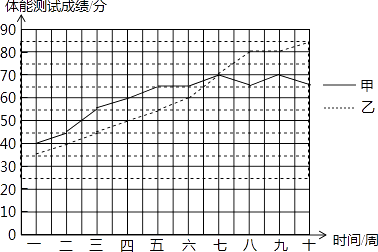
(1)请根据图中所提供的信息填写下表:
平均数 | 中位数 | 体能测试成绩合格次数 | |
甲 | 65 | ||
乙 | 60 |
(2)请从下面两个不同的角度对运动员体能测试结果进行判断: ①依据平均数与成绩合格的次数比较甲和乙,谁的体能测试成绩较好?
②依据平均数与中位数比较甲和乙,谁的体能测试成绩较好?
(3)依据折线统计图和成绩合格的次数,分析哪位运动员体能训练的效果较好.