题目内容
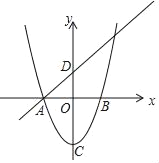
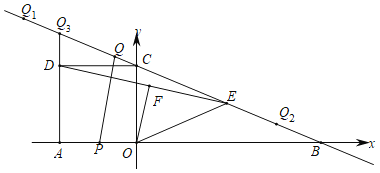
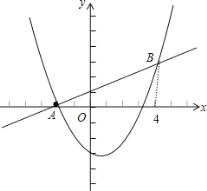
【题目】已知直线l:y=![]() x+1与抛物线y=ax2﹣2x+c(a>0)的一个公共点A恰好在x轴上,点B(4,m)在抛物线上.
x+1与抛物线y=ax2﹣2x+c(a>0)的一个公共点A恰好在x轴上,点B(4,m)在抛物线上.
(Ⅰ)用含a的代数式表示c.
(Ⅱ)抛物线在A,B之间的部分(不包含点A,B)记为图形G,请结合函数图象解答:若图形G在直线l下方,求a的取值范围.
【答案】(Ⅰ)c=﹣4a﹣4;(Ⅱ)0<a≤![]() .
.
【解析】
(1)先利用一次函数解析式求出A点坐标为(﹣2,0),然后把A点坐标代入抛物线解析式即可得到a与c的关系式;
(2)先分别计算出x=4时所对应的一次函数值和二次函数值,然后利用图形G在直线l下方得到12﹣12a≤3,然后解不等式即可.
解:(Ⅰ)当y=0时,![]() x+1=0,解得x=﹣2,则A点坐标为(﹣2,0),
x+1=0,解得x=﹣2,则A点坐标为(﹣2,0),
把A(﹣2,0)代入y=ax2﹣2x+c得4a+4+c=0,
所以c=﹣4a﹣4;
(Ⅱ)当x=4时,y=ax2﹣2x+c=16a﹣8﹣4a﹣4=12a﹣12,则B(4,12a﹣12),
当x=4时,y=![]() x+1=3,
x+1=3,
因为图形G在直线l下方,
所以12﹣12a≤3,
解得a≤![]() ,
,
所以a的取值范围为0<a≤![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目