题目内容
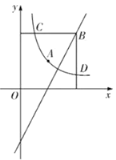
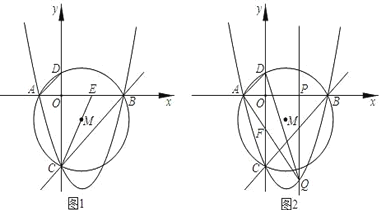
【题目】如图1,已知抛物线y=ax2﹣2x+c(a≠0)与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,﹣3),对称轴是直线x=1,△ACB的外接圆M交y轴的正半轴与点D,连结AD、CM,并延长CM交x轴于点E.
(1)求抛物线的函数表达式和直线BC的函数表达式;
(2)求证:△CAD∽△CEB;
(3)如图2,P为x轴正半轴上的一个动点,OP=t,(0<t<3),过P点与y轴平行的直线交抛物线与点Q,若△QAD的面积为S,写出S与t的函数表达式,问:当t为何值时,△QAD的面积最大,且最大面积为多少?
【答案】(1)![]() ,BC:
,BC:![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ,
,![]() 时,
时,![]() .
.
【解析】
(1)先根据图像得到a,c的值,进而可得到A、B两点的坐标,再求出函数解析式即可;(2)如图,连结AM,根据同弧所对的圆周角相等得到∠ADC=∠ABC=45°,根据圆周角定理可得∠AMC=90°,进而得到∠ACE=45°,所以∠ACD =∠ECB=45°-∠ECD,即可证明△ACD∽△ECB;(3)根据题意易得△AOF∽△APQ,再根据对应边成比例得到OF与PQ的关系,将Q点横坐标代入抛物线方程求出PQ的长度,进而求出OF的长度,再根据S=S△ADF+S△QDF求出S与t的函数表达式,再求出最大值即可.
解:(1)∵抛物线的对称轴是x=1,
∴![]() =1,∴a=1
=1,∴a=1
由图像易知c=-3,所以抛物线解析式为![]() , B(3,0),A(-1,0),C(0,-3)
, B(3,0),A(-1,0),C(0,-3)
设直线BC的函数表达式为:y=kx+b,
则![]() ,解得:k=1,b=-3,
,解得:k=1,b=-3,
∴直线BC的解析式为![]() ;
;
(2)如图,连结AM,
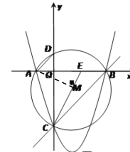
∵OB=OC,∴∠OCB=∠OBC=45°,
∴∠ADC =∠OBC=45°,∠AMC=90°,
又∵AM=CM,∴∠ACE=45°,
∴∠ACD =∠ECB=45°-∠ECD,
∴△ACD∽△ECB
(3)∵PQ∥y轴,∴△AOF∽△APQ,
∴![]() .
.
∴![]() ,
,
∵PQ=![]() ,∴
,∴![]() ,
,
∴S=S△ADF+S△QDF=![]()
![]()
整理得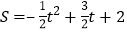 ,
,
化为顶点式得S=﹣![]() (t-
(t-![]() )2+
)2+![]() ,∴当
,∴当![]() .
.