题目内容
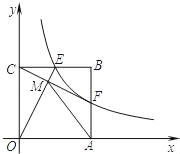
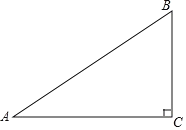
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,
,![]() 的面积是
的面积是![]() .
.
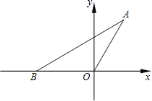
![]() 求点
求点![]() 的坐标;
的坐标;
![]() 求过点
求过点![]() 、
、![]() 、
、![]() 的抛物线的解析式;
的抛物线的解析式;
![]() 在
在![]() 中抛物线的对称轴上是否存在点
中抛物线的对称轴上是否存在点![]() ,使
,使![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
![]() 在
在![]() 中
中![]() 轴下方的抛物线上是否存在一点
轴下方的抛物线上是否存在一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,线段
,线段![]() 把
把![]() 分成两个三角形,使其中一个三角形面积与四边形
分成两个三角形,使其中一个三角形面积与四边形![]() 面积比为
面积比为![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() ;(3)存在,
;(3)存在,![]() .(4)点
.(4)点![]() 坐标是
坐标是![]() .
.
【解析】
(1)由三角形S=![]() OB
OB![]() =
=![]() 可得点B的坐标;
可得点B的坐标;
(2)设抛物线的解析式为y=ax(x+2),点A在其上,求得a;
(3)存在点C、过点A作AF垂直于x轴于点F,抛物线的对称轴x=-1交x轴于点E、当点C位于对称轴与线段AB的交点时,△AOC的周长最小,由三角形相似,得到C点坐标.
(4)设p(x,y),直线AB为y=kx+b,解得k、b,由S四BPOD=S△BPO+S△BOD,S△AOD=S△AOB-S△BOD,两面积正比可知,求出x.
解:![]() 由题意得
由题意得![]() ,
,
∴![]() .
.
![]() 设抛物线的解析式为
设抛物线的解析式为![]() ,代入点
,代入点![]() ,得
,得![]() ,
,
∴![]() ,
,
![]() 存在点
存在点![]() 、过点
、过点![]() 作
作![]() 垂直于
垂直于![]() 轴于点
轴于点![]() ,抛物线
,抛物线
的对称轴![]() 交
交![]() 轴于点
轴于点![]() 、当点
、当点![]() 位于对称轴
位于对称轴
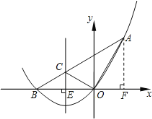
与线段![]() 的交点时,
的交点时,![]() 的周长最小,
的周长最小,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.![]() 存在.如图,设
存在.如图,设![]() ,直线
,直线![]() 为
为![]() ,
,
则![]() ,
,
解得 ,
,
∴直线![]() 为
为![]() ,
,
![]()

![]() ,
,
![]() ,
,
![]() ,
,
∵![]() ,
,
∴ ,
,
∴![]() ,
,![]() (舍去),
(舍去),
∴![]() ,
,
又∵![]() ,
,
∴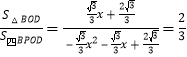 ,
,
∴![]() ,
,![]() .
.
![]() ,不符合题意.
,不符合题意.
∴存在,点![]() 坐标是
坐标是![]() .
.

练习册系列答案
相关题目