题目内容
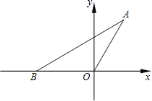
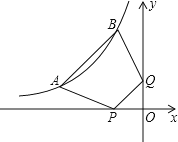
【题目】抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 两点,与
两点,与![]() 交于点
交于点![]() ,且
,且![]() ,则该抛物线的解析式为________.
,则该抛物线的解析式为________.
【答案】![]()
【解析】
根据题意可以求得点C的坐标,然后根据题目中的数据可以求得AC、AB和BC的长,再根据∠ACB=90°,由勾股定理可以求得m的值,然后将A和B的坐标代入函数解析式即可求得二次函数的解析式.
∵抛物线y=ax2+bx2与x轴交于点A(1,0),B(m,0)两点,与y交于点C,
∴点C的坐标为(0,2),
∴AC2=(1)2+(2)2=5,BC2=m2+(2)2=m2+4,AB=m(1)=m+1,
∵∠ACB=90°,
∴AC2+BC2=AB2,
即5+(m2+4)=(m+1)2,
解得m=4,
∴点B的坐标为(4,0),
∴![]() ,
,
解得![]() ,
,
∴二次函数解析式为:y=0.5x21.5x2.
故答案为:y=0.5x21.5x2.

练习册系列答案
相关题目