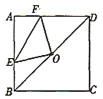
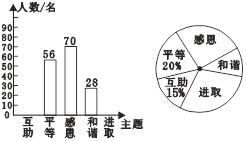题目内容
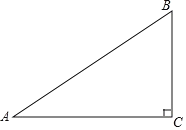
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′E⊥AC时,A′B=_________.
【答案】![]() 或7
或7![]()
【解析】分析:分两种情况:①如图1,作辅助线,构建矩形,先由勾股定理求斜边AB=10,由中点的定义求出AD和BD的长,证明四边形HFGB是矩形,根据同角的三角函数列式可以求DG和DF的长,并由翻折的性质得:∠![]() =∠A,
=∠A, ![]() =AD=5,由矩形性质和勾股定理可以得出结论:
=AD=5,由矩形性质和勾股定理可以得出结论: ![]() =
=![]() ;②如图2,作辅助线,构建矩形
;②如图2,作辅助线,构建矩形![]() ,同理可以求出
,同理可以求出![]() 的长.
的长.
详解:分两种情况:
如图1,过D作DG⊥BC与G,交A′E与F,过B作BH⊥A′E与H,
∵D为AB的中点,
∴BD=![]() AB=AD,
AB=AD,
∵∠C=90,AC=8,BC=6,
∴AB=10,
∴BD=AD=5,
sin∠ABC=![]() ,
,
∴![]() ,
,
∴DG=4,
由翻折得:∠DA′E=∠A,A′D=AD=5,
∴sin∠DA′E=sin∠A=![]() ,
,
∴![]() ,
,
∴DF=3,
∴FG=43=1,
∵A′E⊥AC,BC⊥AC,
∴A′E∥BC,
∴∠HFG+∠DGB=180°,
∵∠DGB=90°,
∴∠HFG=90°,
∵∠EHB=90,
∴四边形HFGB是矩形,
∴BH=FG=1,
同理得:A′E=AE=81=7,
∴A′H=A′EEH=76=1,
在Rt△AHB中,由勾股定理得:A′B=![]() ;
;

②如图2,过D作MN∥AC,交BC与于N,过A′作A′F∥AC,交BC的延长线于F,延长A′E交直线DN于M,
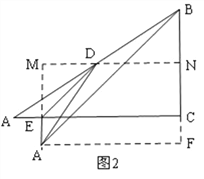
∵A′E⊥AC,
∴A′M⊥MN,A′E⊥A′F,
∴∠M=∠MA′F=90°,
∵∠ACB=90°,
∴∠F=∠ACB=90°,
∴四边形MA′FN是矩形,
∴MN=A′F,FN=A′M,
由翻折得:A′D=AD=5,
Rt△A′MD中,∴DM=3,A′M=4,
∴FN=A′M=4,
Rt△BDN中,∵BD=5,
∴DN=4,BN=3,
∴A′F=MN=DM+DN=3+4=7,
BF=BN+FN=3+4=7,
Rt△ABF中,由勾股定理得:A′B=![]() ;
;
综上所述![]() 的长为
的长为![]() 或
或![]()
故答案为: ![]() 或
或![]() .
.
本题考查的是图形的翻折变换及等腰直角三角形的性质、矩形的性质、平行线分线段成比例定理及勾股定理的综合运用,题型难度较大.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展,某旅游公司对我市一企业个人旅游年消费情况进行问卷调查,随机抽查部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成尚不完整的表和图(如图).
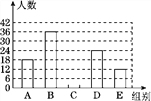
组别 | 个人年消费金额x/元 | 频数(人数) | 频率 |
A | x≤2 000 | 18 | 0.15 |
B | 2 000<x≤4 000 | a | b |
C | 4 000<x≤6 000 | ||
D | 6 000<x≤8 000 | 24 | 0.20 |
E | x>8 000 | 12 | 0.10 |
合计 | c | 1.00 |
根据以上信息回答下列问题:
(1)a=________,b=________,c=________,并将条形统计图补充完整;
(2)在这次调查中,个人年消费金额的中位数出现在________组;
(3)若这个企业有3 000名员工,请你估计个人旅游年消费金额在6 000元以上的人数.