题目内容
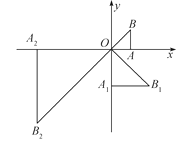
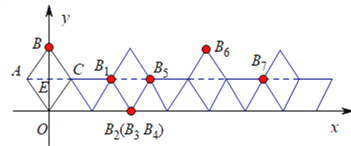
【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1.将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1,B2,B3,…,则B2017的坐标为( )
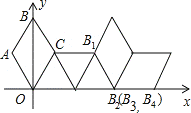
A. (1345,0) B. (1346,0) C. (1345.5,![]() ) D. (1346.5,
) D. (1346.5,![]() )
)
【答案】C
【解析】分析:
如下图,连接AC,由已知易证△ABC是等边三角形,由此可得AC=AB=OA=1,OE=![]() ,CE=
,CE=![]() ,结合图形可得B1、B2、B3、B4、B5、B6的坐标,画出后面的图形,结合图形可知每翻转6次,图形向由平移4个单位,由2017÷6=336……1,可知:点B2017相当于将点B1向右平移了336×4+1.5个单位长度得到的,由此即可得到点B2017的坐标.
,结合图形可得B1、B2、B3、B4、B5、B6的坐标,画出后面的图形,结合图形可知每翻转6次,图形向由平移4个单位,由2017÷6=336……1,可知:点B2017相当于将点B1向右平移了336×4+1.5个单位长度得到的,由此即可得到点B2017的坐标.
详解:
如下图,连接AC交OB于点E,
四边形OABC是菱形,∠ABC=60°,点B在y轴上,OA=1,
∴OA=AB=BC=OC=1,∠ABC=60°,
∴△OAC是等边三角形,∠COE=30°,
∴AC=OA=1,OE=![]() ,CE=
,CE=![]() ,
,
∴由图可知:B1、B2、B3、B4、B5、B6的坐标分别为:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 和
和![]() ;
;
∵由图可知:图形可知每翻转6次,图形向由平移4个单位,而2017÷6=336……1,
∴点B2017相当于将点B1向右平移了336×4+1.5个单位长度得到的,
∴点B2017的坐标为![]() .
.
故选C.

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
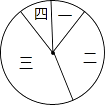
同步奥数系列答案【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).