题目内容
在△ABC中，∠C=40°，高AD，BE所在的直线交于点O，则∠AOB=______．
①高AD，BE所在的直线交于点O在三角形内部，如右图，
∵AD、BE是高，
∴∠BEC=∠ADC=90°，
在四边形CDOE中，∠DOE=360°-∠C-∠BEC-∠ADC=140°，
②高AD，BE所在的直线交于点O在三角形外部，如右图，
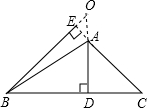∵AD是高，
∴∠ADC=90°，
∵∠C=40°，
∴∠DAC=50°，
∴∠EAO=50°，
∵BE是高，
∴∠AEO=90°，
∴∠AOB=90-∠EAO=90°-50°=40°．
故答案是40°或140°．
∵AD、BE是高，
∴∠BEC=∠ADC=90°，
在四边形CDOE中，∠DOE=360°-∠C-∠BEC-∠ADC=140°，
②高AD，BE所在的直线交于点O在三角形外部，如右图，
∵AD是高，∴∠ADC=90°，
∵∠C=40°，
∴∠DAC=50°，
∴∠EAO=50°，
∵BE是高，
∴∠AEO=90°，
∴∠AOB=90-∠EAO=90°-50°=40°．
故答案是40°或140°．
练习册系列答案
相关题目
