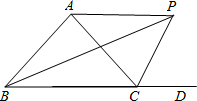
题目内容
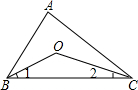
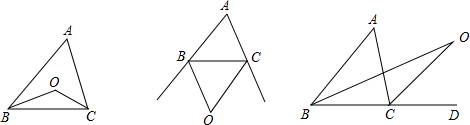
(1)BO、CO分别平分∠ABC和∠ACB,设∠A=n°(n为已知数)求∠O的度数;
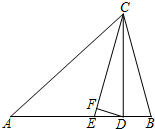
(2)BO、CO分别是△ABC两外角的平分线,设∠A=n°(n为已知数)求∠O的度数;
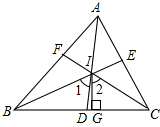
(3)BO、CO分别平分∠ABC和∠ACD,设∠A=n°(n为已知数)求∠O的度数.
(2)BO、CO分别是△ABC两外角的平分线,设∠A=n°(n为已知数)求∠O的度数;
(3)BO、CO分别平分∠ABC和∠ACD,设∠A=n°(n为已知数)求∠O的度数.

(1)根据三角形内角和定理,∠ABC+∠ACB=180°-∠A=180°-n°,
∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
(180°-n°)=90°-
n°,
在△OBC中,∠O=180°-(∠OBC+∠OCB)=180°-(90°-
n°)=90°+
n°;
(2)根据三角形的外角性质,以及角平分线的定义,
∠OBC=
(∠A+∠ACB),∠OCB=
(∠A+∠ABC),
∴∠OBC+∠OCB=
(∠A+∠ACB+∠A+∠ABC)=
(180°+∠A)=90°+
n°,
在△OBC中,∠O=180°-(∠OBC+∠OCB)=180°-(90°+
n°)=90°-
n°;
(3)根据三角形的外角性质,∠ACD=∠A+∠ABC,∠OCD=∠O+∠OBC,
∵BO、CO分别平分∠ABC和∠ACD,
∴∠OBC=
∠ABC,∠OCD=
∠ACD,
∴∠O+
∠ABC=
(∠A+∠ABC),
∴∠O=
∠A=
n°.
∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在△OBC中,∠O=180°-(∠OBC+∠OCB)=180°-(90°-
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据三角形的外角性质,以及角平分线的定义,
∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在△OBC中,∠O=180°-(∠OBC+∠OCB)=180°-(90°+
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据三角形的外角性质,∠ACD=∠A+∠ABC,∠OCD=∠O+∠OBC,
∵BO、CO分别平分∠ABC和∠ACD,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠O+
| 1 |
| 2 |
| 1 |
| 2 |
∴∠O=
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目