Question

【题目】在平面直角坐标系xOy中，对于点和点，给出如下定义：若，则称点为点的限变点．例如：点的限变点的坐标是，点的限变点的坐标是．

（1）①点的限变点的坐标是___________；

②在点，中有一个点是函数图象上某一个点的限变点，这个点是_______________；

（2）若点在函数的图象上，其限变点的纵坐标的取值范围是，求的取值范围；

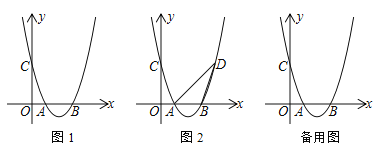
（3）若点在关于的二次函数的图象上，其限变点的纵坐标的取值范围是或，其中．令，求关于的函数解析式及的取值范围．

Answer 1

【答案】（1）①；② 点B．（2）（3）

【解析】

（1）①根据限变点的定义可判断点的限变点的坐标是；②求出点，的原始点，代入，适合解析式的是点B的限变点；（2）根据，可得图象上的点P的限变点必在函数的图象上，求出当时和当时，x的值，再由推出；（3）确定出的顶点坐标，然后分和两种情况讨论：其中，不合题意，时，求出，所以，然后可确定的取值范围是≥2．

解：（1）①；

② 点B．

（2）依题意，图象上的点P的限变点必在函数的图象上．

，即当时，取最大值2．

当时，或．

或（舍）．

当时， 或．

或．

，

由图象可知，的取值范围是．

（3），

顶点坐标为．

若，的取值范围是或，与题意不符．

若，当时，的最小值为，即；

当时，的值小于，即．

．

关于的函数解析式为．

当t=1时，取最小值2．

的取值范围是≥2．