Question

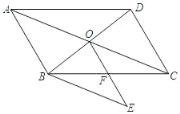
【题目】如图，CD为⊙O的直径，弦AB⊥CD，垂足为E，，CE=1，AB=6，则弦AF的长度为___.

Answer 1

【答案】

【解析】

连接OA、OB，OB交AF于G，如图，利用垂径定理得到AE=BE=3，设⊙O的半径为r，则OE=r-1，OA=r，根据勾股定理得到，解得r=5，再利用垂径定理得到OB⊥AF，AG=FG，则，，然后解方程组求出AG，从而得到AF的长．

连接OA、OB，OB交AF于G，如图，

∵AB⊥CD，

∴AE=BE=AB=3，

设⊙O的半径为r，则OE=r1，OA=r，

在Rt△OAE中,32+(r1)2=r2，解得r=5，

∵弧AB=弧BF，

∴OB⊥AF，AG=FG，

在Rt△OAG中,AG2+OG2=52，①

在Rt△ABG中,AG2+(5OG)2=62，②

解由①②组成的方程组得到AG=，

∴AF=2AG=.

故答案为.