题目内容
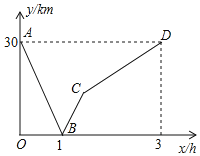
【题目】如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.

(1)在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长.
②当A,D,M三点为同一直角三角形的顶点时,求AM的长.
(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2,如图2,此时∠AD2C=135°,CD2=60,求BD2的长.
【答案】(1)①20;②20![]() 或10
或10![]() ;(2)30
;(2)30![]()
【解析】
(1)①根据D在AM上还是AM的延长线上分两种情况求解即可.
②由图可知∠MAD不能为直角,当∠AMD或∠ADM=90为直角时,分别应用勾股定理解答即可.
(2)连接CD,先用勾股定理求出CD1,再利用全等三角形的性质证明BD2= CD1即可.
(1)①AM=AD+DM=40,或AM=AD﹣DM=20.
②显然∠MAD不能为直角.
当∠AMD为直角时,AM2=AD2﹣DM2=302﹣102=800,
∴AM=20![]() 或(﹣20
或(﹣20![]() 舍弃).
舍弃).
当∠ADM=90°时,AM2=AD2+DM2=302+102=1000,
∴AM=10![]() 或(﹣10
或(﹣10![]() 舍弃).
舍弃).
综上所述,满足条件的AM的值为20![]() 或10
或10![]() .
.
(2)如图2中,连接CD.
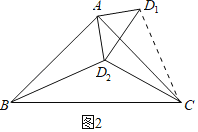
由题意:∠D1AD2=90°,AD1=AD2=30,
∴∠AD2D1=45°,D1D2=30![]() ,
,
∵∠AD2C=135°,
∴∠CD2D1=90°,
∴CD1=![]() =30
=30![]() ,
,
∵∠BAC=∠A1AD2=90°,
∴∠BAC﹣∠CAD2=∠D2AD1﹣∠CAD2,
∴∠BAD2=∠CAD1,
∵AB=AC,AD2=AD1,
∴△BAD2≌△CAD1(SAS),
∴BD2=CD1=30![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】公司以10元/千克的价格收购一批产品进行销售,经过市场调查获悉,日销售量y(千克)是销售价格x(元/千克)的一次函数,部分数据如表:
销售价格x(元/千克) | 10 | 15 | 20 | 25 | 30 |
日销售量y(千克) | 300 | 225 | 150 | 75 | 0 |
(1)直接写出y与x之间的函数表达式;
(2)求日销售利润为150元时的销售价格;
(3)若公司每销售1千克产品需另行支出a元(0<a<10)的费用,当20≤x≤25时,公司的日获利润的最大值为1215元,求a的值.