题目内容
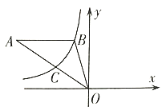
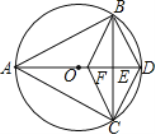
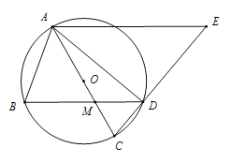
【题目】如图,ABD内接于半径为5的⊙O,连结AO并延长交BD于点M,交圆⊙O于点C,过点A作AE//BD,交CD的延长线于点E,AB=AM.
(1)求证:ABM∽ECA.
(2)当CM=4OM时,求BM的长.
(3)当CM=kOM时,设ADE的面积为![]() , MCD的面积为
, MCD的面积为![]() ,求
,求![]() 的值(用含k的代数式表示).
的值(用含k的代数式表示).
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用同弧所对的圆周角相等,以及平行线的性质得出角相等,再利用两角对应相等的两个三角形相似解题.
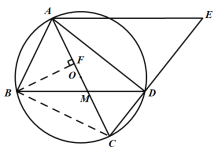
(2)连接BC构造直角三角形,再过B作BF⊥AC,利用所得到的直角三角形,结合勾股定理解题.
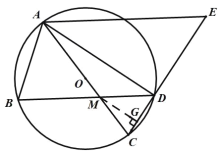
(3)过点M作出△MCD的高MG, 再由![]() ,
,![]() 得出线段间的比例关系,从而可得出结果.
得出线段间的比例关系,从而可得出结果.
解:(1)∵弧CD=弧CD,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]()
∵弧AD=弧AD
∴![]()
∴![]()
(2)连接BC,作![]() ,
,
∵![]() 半径为5,
半径为5,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
由图可知AC为直径,![]() ,得
,得![]() .
.
![]() ,解得
,解得![]() .
.
在![]() 中,
中,![]() ,则
,则![]() .
.
∴![]() .
.
在![]() 中,
中,![]() .
.
(3)当![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
过M作![]() ,
,![]() ,(以AC为直径),
,(以AC为直径),
可知![]() ,
,
∴![]() .
.
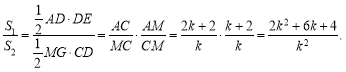

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目