题目内容
【题目】如图，双曲线
经过
的顶点
和
上的中点
，
轴，点的坐标为
．则（1）点的坐标为______．（2）的面积是_______．
【答案】
【解析】
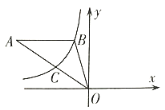
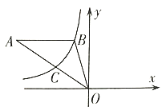
（1）由AB∥x轴，点B的坐标为（-1，4），可设A（x，4），由OA边上的中点是C，可得点C的坐标为（
x，2），根据双曲线y=
（x＜0）经过点B和点C，列出方程求出x的值即可；
（2）根据A、B两点的坐标求出AB的长以及AB边上的高，根据三角形面积公式即可求出三角形OAB的面积．
解：（1）∵AB∥x轴，点B的坐标为（-1，4），
∴可设A（x，4），
∵OA边上的中点是C，
∴点C的坐标为（x，2），
∵双曲线y=（x＜0）经过点B和点C，
∴x×2=-1×4，
∴x=-4，
∴点C的坐标为（-2，2），
故答案为：（-2，2）；
（2）∵A（-4，4），B（-1，4），
∴AB=-1-（-4）=3，AB边上的高为4，
∴△OAB的面积是：×3×4=6．
故答案为：6．
练习册系列答案
相关题目
