题目内容
【题目】如图,已知E、F分别是ABCD的边BC,AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=8,∠BAC=90°,求BE的长.

【答案】(1)证明见解析;(2)4.
【解析】
(1)利用平行四边形的性质得出AF∥EC,再得出AF=EC,即可证明四边形AECF是平行四边形;
(2)利用菱形的性质以及三角形内角和定理得出∠1=∠2,进而求出∠3=∠4,再利用直角三角形的性质得出答案.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC,
∴AF∥EC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形;
(2)如图,
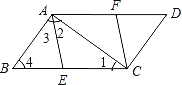
∵四边形AECF是菱形,
∴AE=EC,
∴∠1=∠2,
∵∠BAC=90°,
∴∠3=90°﹣∠2,∠4=90°﹣∠1,
∴∠3=∠4,
∴AE=BE,
∴BE=AE=CE=![]() BC=4.
BC=4.

练习册系列答案
相关题目