题目内容
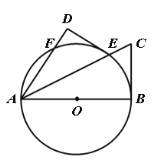
【题目】如图,已知在正方形ABCD中,对角线AC与BD相交于点O,AE,DF分别是∠OAD与∠ODC的平分线,AE的延长线与DF相交于点G,则下列结论:①AG⊥DF;②EF∥AB;③AB=AF;④AB=2EF.其中正确的结论是( )
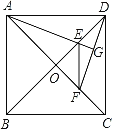
A.①②B.③④C.①②③D.①②③④
【答案】C
【解析】
①证明∠DAE=∠CDF,进而得∠DAF+∠ADG=90°,便可判断①的正误;
②证明△AGF≌△AGD(ASA),得AG垂直平分DF,得ED=EF,得∠EFD=∠EDF=∠CDF,得EF∥CD,便可判断②的正误;
③由△AGF≌△AGD得AF=AD,便可判断③的正误;
④证明EF=ED=![]() ,由平行于三角形一边的直线所截得的三角形的三边与原三角形的三边对应成比例便可得AB与EF的数量关系,进而判断④的正误.
,由平行于三角形一边的直线所截得的三角形的三边与原三角形的三边对应成比例便可得AB与EF的数量关系,进而判断④的正误.
解:①∵四边形ABCD是正方形,
∴∠CAD=∠BDC=45°,
∵AE,DF分别是∠OAD与∠ODC的平分线,
∴∠DAE=∠CDF,
∵∠ADF+∠CDF=90°,
∴∠DAF+∠ADG=90°,
∴∠AGD=90°,即AG⊥DF,
故①结论正确;
②在△AGF和△AGD中,
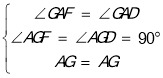 ,
,
∴△AGF≌△AGD(ASA),
∴GF=GD,
∵AG⊥DF,
∴EF=ED,
∴∠EFD=∠EDF=∠CDF,
∴EF∥CD∥AB,
故②正确;
③∵△AGF≌△AGD(ASA),
∴AD=AF=AB,
故③正确;
④∵EF∥CD,
∴∠OEF=∠ODC=45°,
∵∠COD=90°,
∴EF=ED=![]() ,
,
∴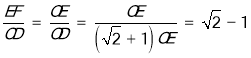 ,
,
∴AB=CD=(![]() +1)EF,
+1)EF,
故④错误.
故选:C.

【题目】某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如下两幅不完整的统计图表,请根据图表信息回答下列问题:
![]()
类别 | 项 目 | 人数 |
A | 跳绳 | 59 |
B | 健身操 | ▲ |
C | 俯卧撑 | 31 |
D | 开合跳 | ▲ |
E | 其它 | 22 |

(1)求参与问卷调查的学生总人数.
(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数.