ЬтФПФкШн
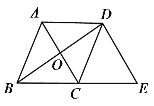
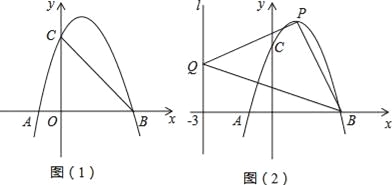
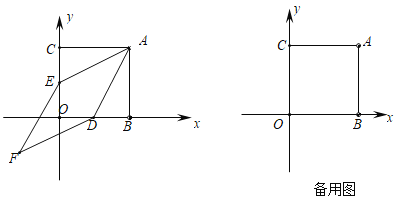
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌе§ЗНаЮABOCЕФСНжБНЧБпЗжБ№дкзјБъжсЕФе§АыжсЩЯЃЌЗжБ№Й§OBЃЌOCЕФжаЕуDЃЌEзїAEЃЌADЕФЦНааЯпЃЌЯрНЛгкЕуFЃЌ вбжЊOB=8ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮAEFDЮЊСтаЮЃЎ
ЃЈ2ЃЉЧѓЫФБпаЮAEFDЕФУцЛ§ЃЎ
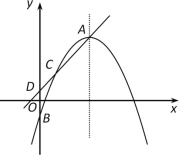
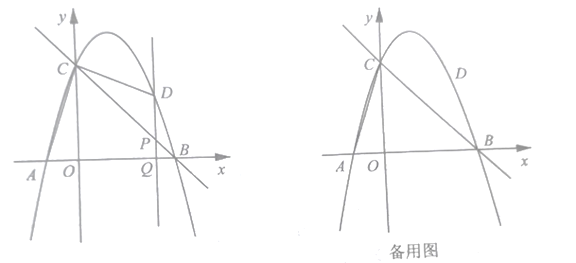
ЃЈ3ЃЉШєЕуPдкxжсе§АыжсЩЯ(вьгкЕуD)ЃЌЕуQдкyжсЩЯЃЌЦНУцФкЪЧЗёДцдкЕуGЃЌЪЙЕУвдЕуAЃЌPЃЌ QЃЌGЮЊЖЅЕуЕФЫФБпаЮгыЫФБпаЮAEFDЯрЫЦЃПШєДцдкЃЌЧѓЕуPЕФзјБъЃЛШєВЛДцдкЃЌЪдЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉ48ЃЛЃЈ3ЃЉЕуPЕФзјБъЮЊ(12ЃЌ0)ЃЌ(24ЃЌ0)ЃЌ(![]() ЃЌ0)ЃЌ(
ЃЌ0)ЃЌ(![]() ЃЌ0)ЃЌ(16ЃЌ0)
ЃЌ0)ЃЌ(16ЃЌ0)
ЁОНтЮіЁП
ЃЈ1ЃЉНсКЯе§ЗНаЮаджЪЧѓЕУЁїACEЁеЁїABDЃЌДгЖјЕУЕНAE=ADЃЌИљОнСкБпЯрЕШЕФЦНааЫФБпаЮЪЧСтаЮжЄУїМДПЩЃЎ
ЃЈ2ЃЉСЌНгDEЃЌЧѓГіЁїADEЕФУцЛ§МДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉЪзЯШжЄУїAK=3DKЃЌЂйЕБAPЮЊСтаЮЕФвЛБпЃЌЕуQдкxжсЕФЩЯЗНЃЌгаЭМ2ЃЌЭМ3СНжжЧщаЮЃЎЂкЕБAPЮЊСтаЮЕФБпЃЌЕуQдкxжсЕФЯТЗНЪБЃЌгаЭМ4ЃЌЭМ5СНжжЧщаЮЃЎЂлШчЭМ6жаЃЌЕБAPЮЊСтаЮЕФЖдНЧЯпЪБЃЌгаЭМ6вЛжжЧщаЮЃЎЗжБ№РћгУЯрЫЦШ§НЧаЮЕФаджЪЧѓНтМДПЩЃЎ
ЃЈ1ЃЉЁпDFЁЮAEЃЌEFЁЮADЃЌ
ЁрЫФБпаЮAEFDЪЧЦНааЫФБпаЮ.
ЁпЫФБпаЮABOCЪЧе§ЗНаЮЃЌ
ЁрOBЃНOCЃНABЃНACЃЌЁЯACEЃНЁЯABDЃН90Ёу.
ЁпЕуDЃЌEЪЧOBЃЌOCЕФжаЕуЃЌ
ЁрCEЃНBDЃЌ
ЁрЁїACEЁеЁїABD(SAS)ЃЌ
ЁрAEЃНADЃЌ
Ёр![]() ЪЧСтаЮ
ЪЧСтаЮ
ЃЈ2ЃЉШчЭМ1ЃЌСЌНсDE
ЁпSЁїABDЃН![]() ABЁЄBDЃН
ABЁЄBDЃН![]() ЃЌ SЁїODEЃН
ЃЌ SЁїODEЃН![]() ODЁЄOEЃН
ODЁЄOEЃН![]() ЃЌ
ЃЌ
ЁрSЁїAEDЃНSе§ЗНаЮABOCЃ2 SЁїABDЃ SЁїODEЃН64Ѓ2![]() Ѓ8ЃН24ЃЌ
Ѓ8ЃН24ЃЌ
ЁрSСтаЮAEFDЃН2SЁїAEDЃН48
ЃЈ3ЃЉгЩЭМ1ЃЌСЌНсAFгыDEЯрНЛгкЕуKЃЌвзЕУЁїADKЕФСНжБНЧБпжЎБШЮЊ1:3
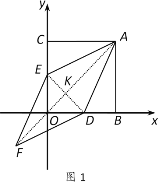
1ЃЉЕБAPЮЊСтаЮвЛБпЪБЃЌЕуQдкxжсЩЯЗНЃЌгаЭМ2ЁЂЭМ3СНжжЧщПіЃК
ШчЭМ2ЃЌAGгыPQНЛгкЕуHЃЌ
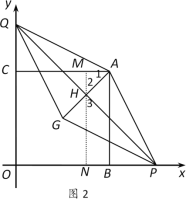
ЁпСтаЮPAQGЁзСтаЮADFEЃЌ
ЁрЁїAPHЕФСНжБНЧБпжЎБШЮЊ1:3
Й§ЕуHзїHNЁЭxжсгкЕуNЃЌНЛACгкЕуMЃЌЩшAM=t
ЁпHNЁЮOQЃЌЕуHЪЧPQЕФжаЕуЃЌ
ЁрЕуNЪЧOPжаЕуЃЌ
ЁрHNЪЧЁїOPQЕФжаЮЛЯпЃЌ
ЁрONЃНPNЃН8Ѓt
гжЁпЁЯ1ЃНЁЯ3ЃН90ЁуЃЁЯ2ЃЌЁЯPNHЃНЁЯAMHЃН90ЁуЃЌ
ЁрЁїHMAЁзЁїPNHЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрHNЃН3AMЃН3tЃЌ
ЁрMHЃНMNЃNHЃН8Ѓ3t.
ЁпPNЃН3MHЃЌ
Ёр8Ѓt =3(8Ѓ3t)ЃЌНтЕУtЃН2
ЁрOPЃН2ONЃН2(8Ѓt)ЃН12
ЁрЕуPЕФзјБъЮЊ(12ЃЌ0)
ШчЭМ3ЃЌЁїAPHЕФСНжБНЧБпжЎБШЮЊ1:3
Й§ЕуHзїHIЁЭyжсгкЕуIЃЌЙ§ЕуPзїPNЁЭxжсНЛIHгкЕуNЃЌбгГЄBAНЛINгкЕуM
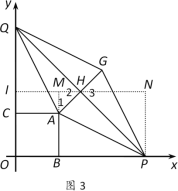
ЁпЁЯ1ЃНЁЯ3ЃН90ЁуЃЁЯ2ЃЌЁЯAMHЃНЁЯPNHЃЌ
ЁрЁїAMHЁзЁїHNPЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌЩшMHЃНtЃЌ
ЃЌЩшMHЃНtЃЌ
ЁрPNЃН3MHЃН3tЃЌ
ЁрAMЃНBMЃABЃН3tЃ8ЃЌ
ЁрHNЃН3AMЃН3(3tЃ8) ЃН9tЃ24
гжЁпHIЪЧЁїOPQЕФжаЮЛЯпЃЌ
ЁрOPЃН2IHЃЌ
ЁрHIЃНHNЃЌ
Ёр8ЃЋtЃН9tЃ24ЃЌНтЕУ tЃН4
ЁрOPЃН2HIЃН2(8ЃЋt)ЃН24ЃЌ
ЁрЕуPЕФзјБъЮЊ(24ЃЌ0)
2ЃЉЕБAPЮЊСтаЮвЛБпЪБЃЌЕуQдкxжсЯТЗНЃЌгаЭМ4ЁЂЭМ5СНжжЧщПіЃК
ШчЭМ4ЃЌЁїPQHЕФСНжБНЧБпжЎБШЮЊ1:3
Й§ЕуHзїHMЁЭyжсгкЕуMЃЌЙ§ЕуPзїPNЁЭHMгкЕуN
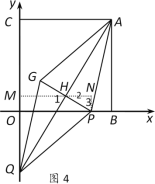
ЁпMHЪЧЁїQACЕФжаЮЛЯпЃЌ
ЁрHMЃН![]() ЃН4
ЃН4
гжЁпЁЯ1ЃНЁЯ3ЃН90ЁуЃЁЯ2ЃЌЁЯHMQЃНЁЯNЃЌ
ЁрЁїHPNЁзЁїQHMЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌдђPNЃН
ЃЌдђPNЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрOMЃН![]()
ЩшHNЃНtЃЌдђMQЃН3t
ЁпMQЃНMCЃЌ
Ёр3tЃН8Ѓ![]() ЃЌНтЕУtЃН
ЃЌНтЕУtЃН![]()
ЁрOPЃНMNЃН4ЃЋtЃН![]() ЃЌ
ЃЌ
ЁрЕуPЕФзјБъЮЊ(![]() ЃЌ0)
ЃЌ0)
ШчЭМ5ЃЌЁїPQHЕФСНжБНЧБпжЎБШЮЊ1:3
Й§ЕуHзїHMЁЭxжсгкЕуMЃЌНЛACгкЕуIЃЌЙ§ЕуQзїNQЁЭHMгкЕуN

ЁпIHЪЧЁїACQЕФжаЮЛЯпЃЌ
ЁрCQЃН2HIЃЌNQЃНCIЃН4
ЁпЁЯ1ЃНЁЯ3ЃН90ЁуЃЁЯ2ЃЌЁЯPMHЃНЁЯQNHЃЌ
ЁрЁїPMHЁзЁїHNQЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌдђMHЃН
ЃЌдђMHЃН![]() NQЃН
NQЃН![]()
ЩшPMЃНtЃЌдђHNЃН3tЃЌ
ЁпHNЃНHIЃЌ
Ёр3tЃН8+![]() ЃЌНтЕУ tЃН
ЃЌНтЕУ tЃН![]()
ЁрOPЃНOMЃPMЃНQNЃPMЃН4ЃtЃН![]() ЃЌ
ЃЌ
ЁрЕуPЕФзјБъЮЊ(![]() ЃЌ0)
ЃЌ0)
3ЃЉЕБAPЮЊСтаЮЖдНЧЯпЪБЃЌгаЭМ6вЛжжЧщПіЃК
ШчЭМ6ЃЌЁїPQHЕФСНжБНЧБпжЎБШЮЊ1:3
Й§ЕуHзїHMЁЭyжсгкЕуMЃЌНЛABгкЕуIЃЌЙ§ЕуPзїPNЁЭHMгкЕуN
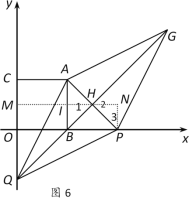
ЁпHIЁЮxжсЃЌЕуHЮЊAPЕФжаЕуЃЌ
ЁрAIЃНIBЃН4ЃЌ
ЁрPNЃН4
ЁпЁЯ1ЃНЁЯ3ЃН90ЁуЃЁЯ2ЃЌЁЯPNHЃНЁЯQMHЃН90ЁуЃЌ
ЁрЁїPNHЁзЁїHMQЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌдђMHЃН3PNЃН12ЃЌHIЃНMHЃMIЃН4
ЃЌдђMHЃН3PNЃН12ЃЌHIЃНMHЃMIЃН4
ЁпHIЪЧЁїABPЕФжаЮЛЯпЃЌ
ЁрBPЃН2HIЃН8ЃЌМДOPЃН16ЃЌ
ЁрЕуPЕФзјБъЮЊ(16ЃЌ0)
злЩЯЫљЪіЃЌЕуPЕФзјБъЮЊ(12ЃЌ0)ЃЌ(24ЃЌ0)ЃЌ(![]() ЃЌ0)ЃЌ(
ЃЌ0)ЃЌ(![]() ЃЌ0)ЃЌ(16ЃЌ0)ЃЎ
ЃЌ0)ЃЌ(16ЃЌ0)ЃЎ